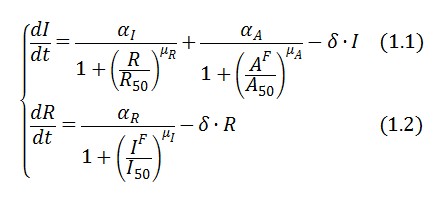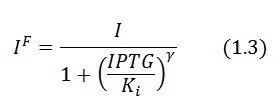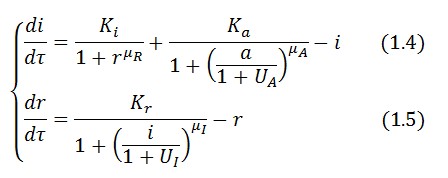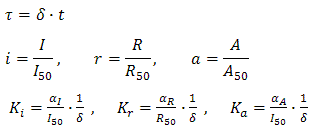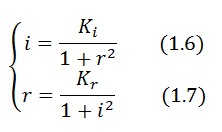"
Team:Bologna/Modeling
From 2008.igem.org
| HOME | TEAM | PROJECT | MODELING | WET-LAB | SOFTWARE | SUBMITTED PARTS | BIOSAFETY AND PROTOCOLS |
|---|
Contents |
Model-based analysis of the genetic Flip-Flop
Mathematical Model
Dimensional equations
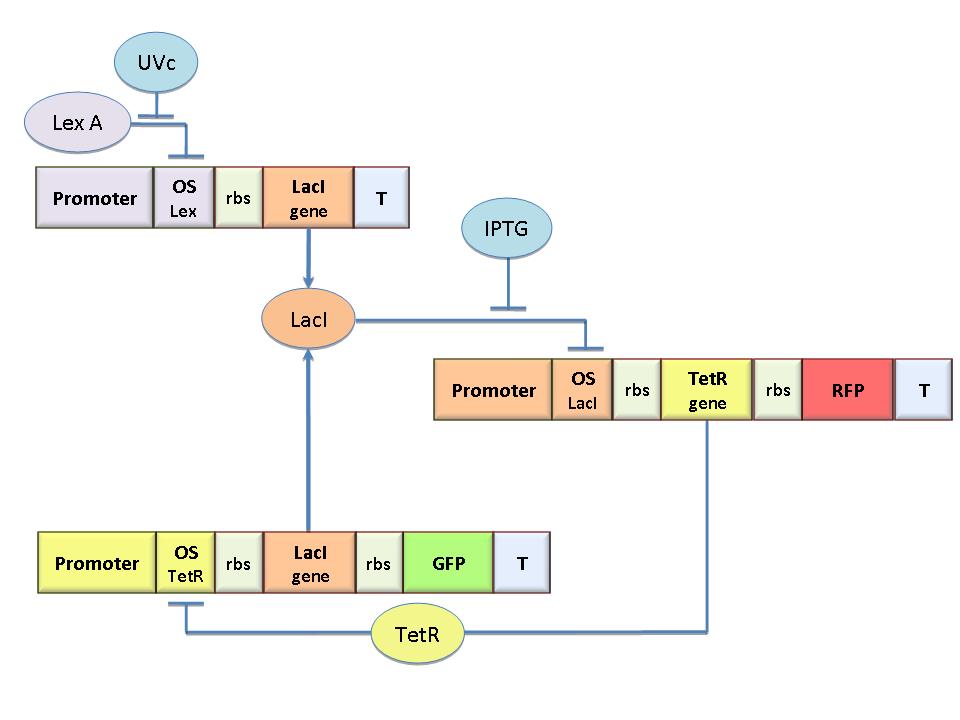
The molecular circuit in Figure 1 works as a Flip-Flop (SR Latch), which can switch between two different states according to the external stimuli (UVc and IPTG).
The molecular circuit show two possible stable state: LacION and TetRON.
The circuit can be modeled by the following equations:
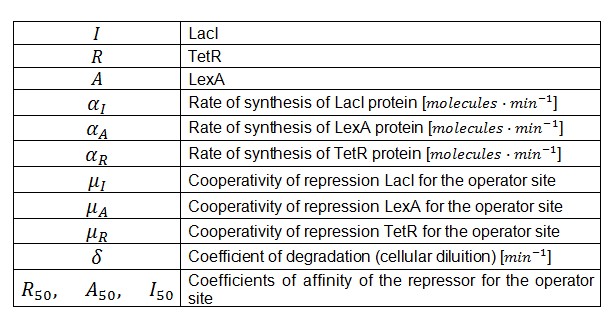
Symbols and parameters are defined in Table 1:
- A common motif in repressor proteins is the presence of a dimeric nucleotide binding site. In accordance to this general structure the cooperativity coefficients () were assumed equal to 2.
In the model we distinguish between LacI protein binded to repressor IPTG 
and protein free 
.
Since 
and considering the law of mass action 
we can write:
Adimensional equations
The equations (1.1) and (1.2) were modified to an adimensional form:
where:
Equibrium conditions
At equilibrium and in absence of stimuli, the adimensional concentrations of LacI (i) and TetR (r) are related by the equation:
To obtain these equations the second term in equation (1.5)was ignored (). This is justified by the high binding constant of LexA for its operator, and the consequent low production of LacI (see Figure 1).
Stability analysis
Assuming as starting condition the LacION state (Figure 1) its stability is guaranteed if the adimensional concentration of LacI is higher than 1 (Figure 2).
In the limit of (), equation (1.7) simplifies:
Experimental identification
The MAVs were identified comparing the experimental response of the genetic circuits in Figure
