Team:Paris/Analysis/Math+Sim
From 2008.igem.org
(→Oscillations) |
(→System analysis) |
||
| Line 87: | Line 87: | ||
| style=" text-align:center;" |[[Image:Core0.png|150px|center]] | | style=" text-align:center;" |[[Image:Core0.png|150px|center]] | ||
| style=" text-align:center;" |[[Image:orgsad.gif]] | | style=" text-align:center;" |[[Image:orgsad.gif]] | ||
| - | | Non oscillating system | + | | Non oscillating system. |
|- style="background: #dddddd;" | |- style="background: #dddddd;" | ||
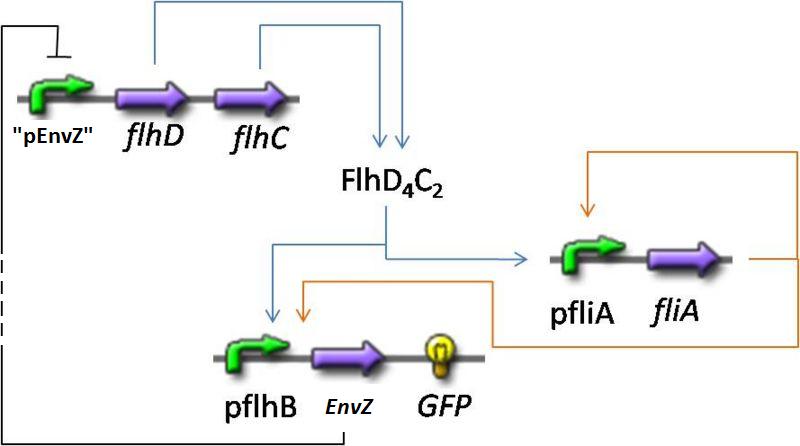
| style="background: #D4E2EF;" |Removing the activation of envZ via FlhDC | | style="background: #D4E2EF;" |Removing the activation of envZ via FlhDC | ||
| Line 93: | Line 93: | ||
| style=" text-align:center;" |[[Image:Core1.png|150px|center]] | | style=" text-align:center;" |[[Image:Core1.png|150px|center]] | ||
| style=" text-align:center;" |[[Image:Orgstar.gif]] | | style=" text-align:center;" |[[Image:Orgstar.gif]] | ||
| - | | | + | | Non oscillating system. Activation of envZ via FlhDC has a negative effect on the presence of oscillations. This interaction creates a 'shortcut' in the loop, diminishing the effect of Flia in the system. This interaction is already low in the core system, removing it has a moderate positive effect. |
|- style="background: #dddddd;" | |- style="background: #dddddd;" | ||
| style="background: #D4E2EF;" |Removing the auto-activation of flia | | style="background: #D4E2EF;" |Removing the auto-activation of flia | ||
| Line 99: | Line 99: | ||
| style=" text-align:center;" |[[Image:Core2.png|150px|center]] | | style=" text-align:center;" |[[Image:Core2.png|150px|center]] | ||
|style=" text-align:center;" | [[Image:Orgstar.gif]][[Image:Orgstar.gif]] | |style=" text-align:center;" | [[Image:Orgstar.gif]][[Image:Orgstar.gif]] | ||
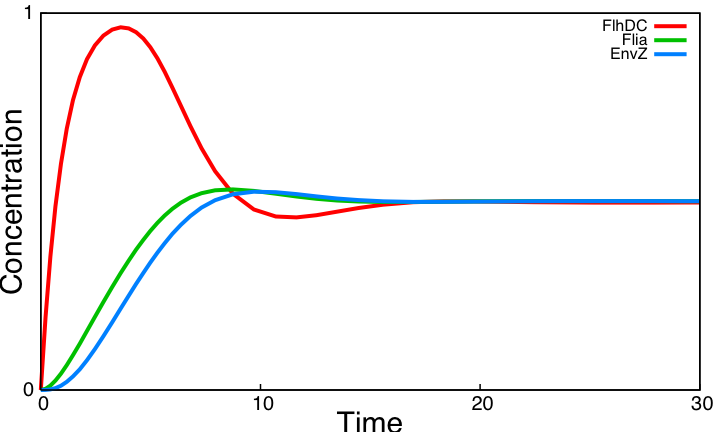
| - | | Damped oscillations | + | | Damped oscillations. Auto-activation of Flia slows its dynamic. For oscillation to appear, different species need to have comparable time scales : oscillations are much more easier without Flia auto-activation. |
|- style="background: #dddddd;" | |- style="background: #dddddd;" | ||
| style="background: #D4E2EF;" |Removing both: the activation of envZ via FlhDC and the auto-activation of flia | | style="background: #D4E2EF;" |Removing both: the activation of envZ via FlhDC and the auto-activation of flia | ||
| Line 116: | Line 116: | ||
|}</center> | |}</center> | ||
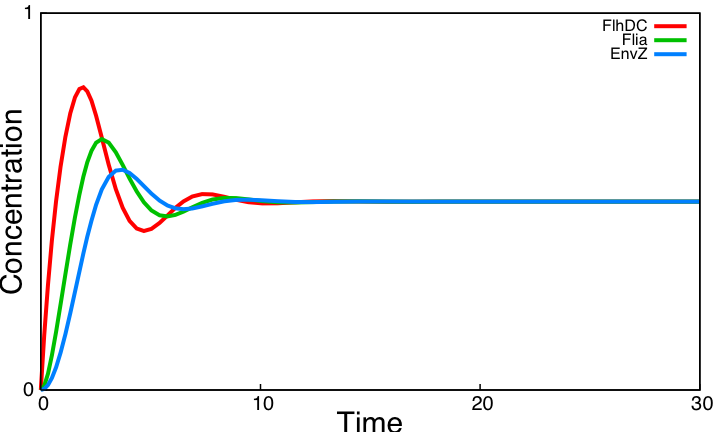
| - | This analysis shows that the core system and its altered variants | + | This analysis shows that the core system and its altered variants can only provide damped oscillations. In the next section, we examine more significant topology improvements of the core system. |
= Navigator = | = Navigator = | ||
Revision as of 16:09, 26 October 2008
|
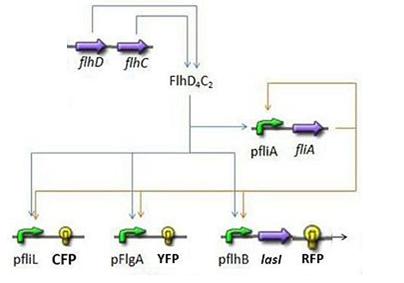
Mathematical analysis and simulations
FIFO
where CFP, YFP, and RFP will be denoted below as respectively Z1,Z2 and Z3.
We have implemented this system using Matlab (see the corresponding codes)
Indeed, we may see that there is a LIFO behavior rather than the FIFO we expect...
Oscillations
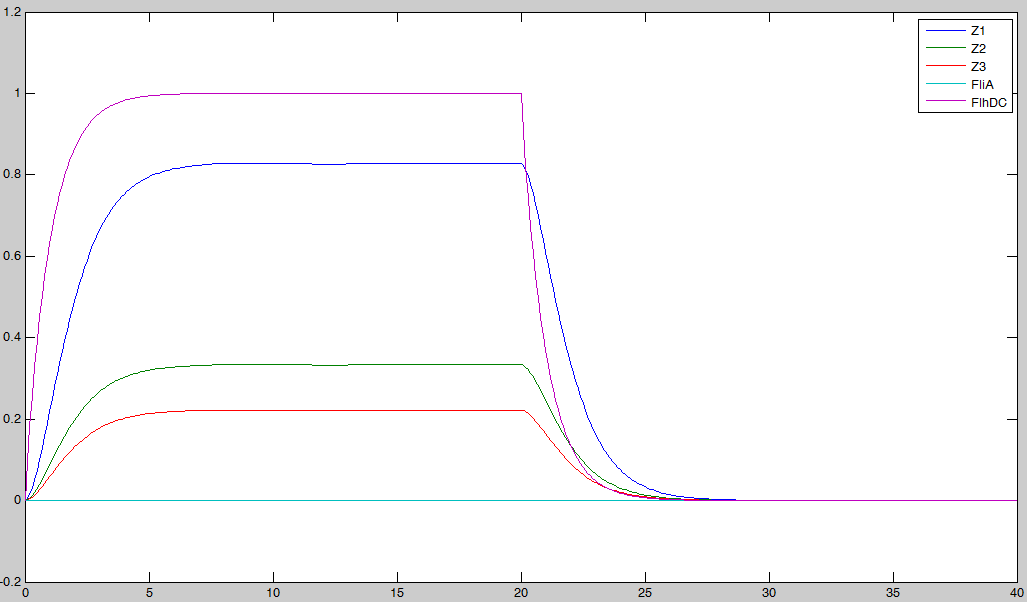
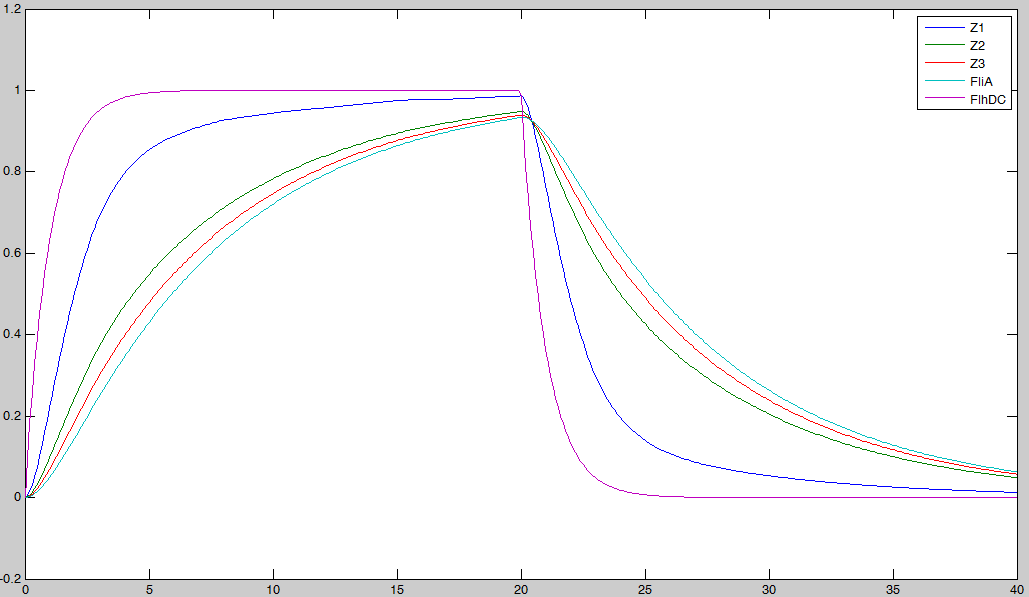
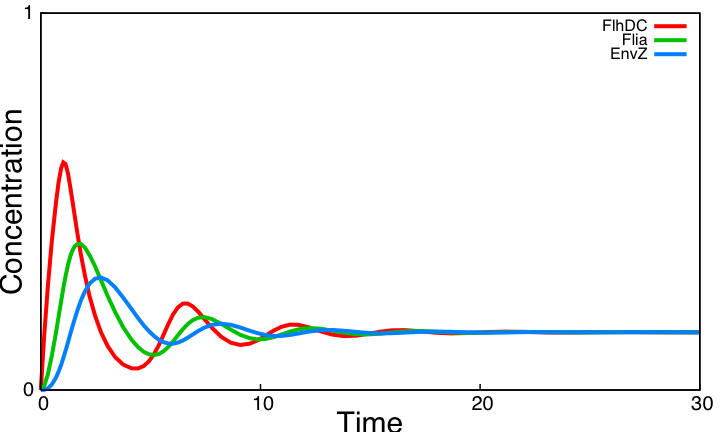
If you want more details about the way we have built them, you can go to the model construction page. If one tries to draw simulations of this system, he will obtain this kind of results : In a nutshell : It does not work !
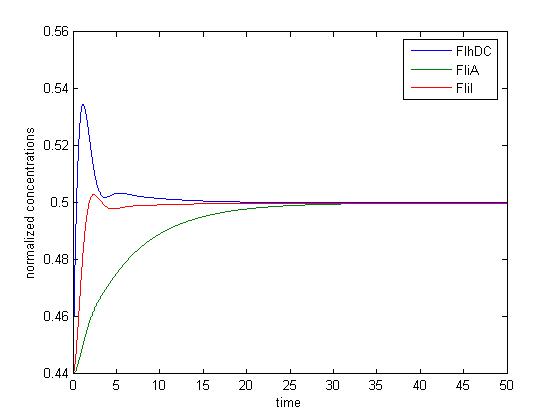
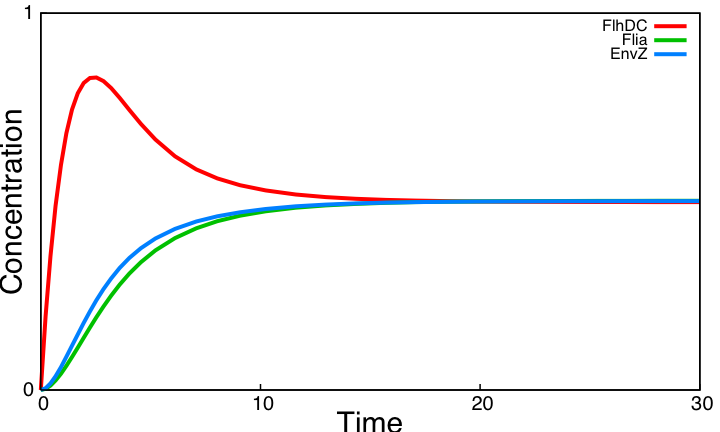
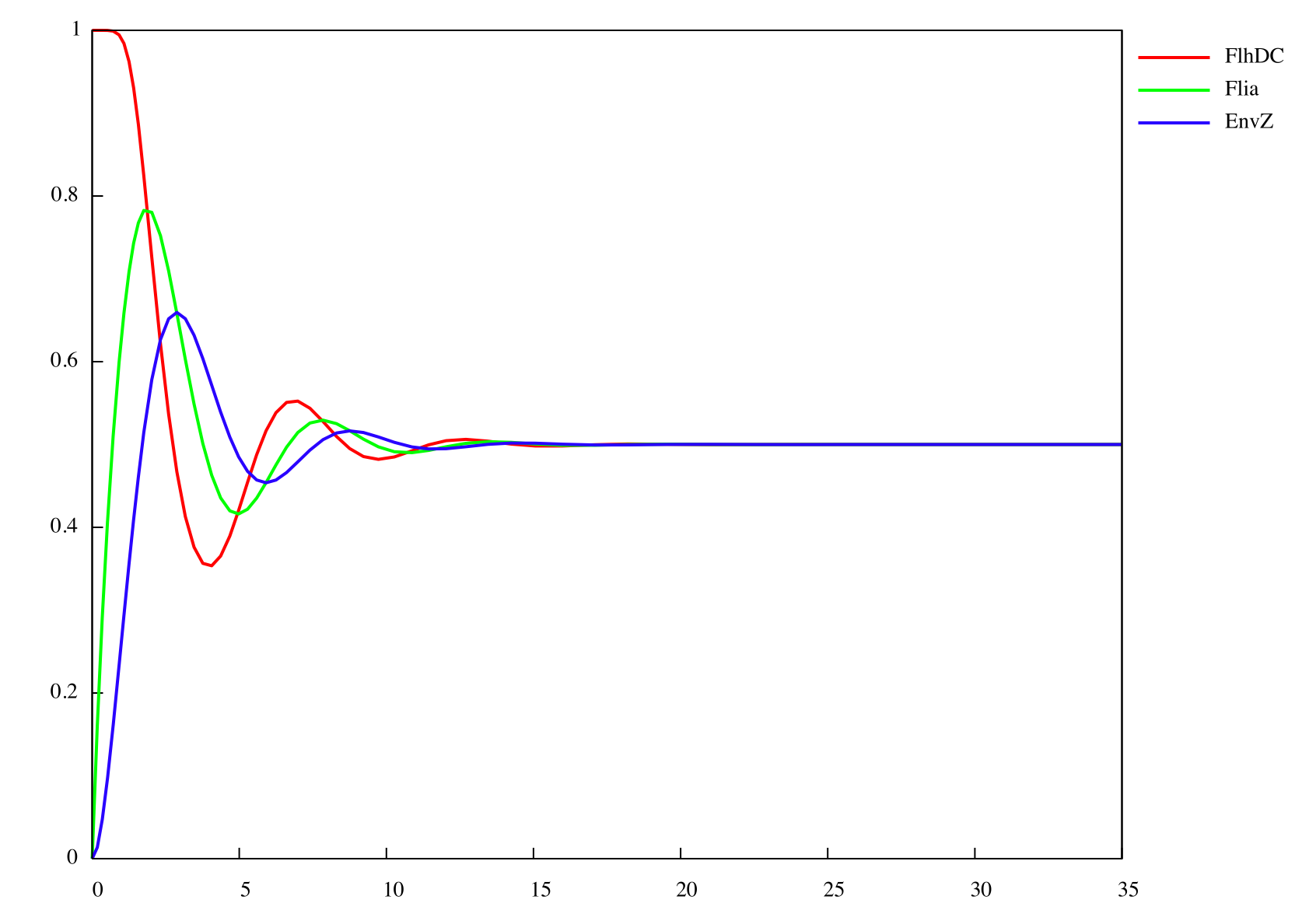
Finally, the logical continuation of the process will be to try to improve the biological system in order to find oscillations. This will be described in the part below, as well as in the section System Improvements. System analysisSimulations of the core system displayed above reveal that it does not exhibit an oscillatory behavior. In this section we use the model of the core system to try to figure out the contribution of some key characteristics of the network topology on the dynamic of the system. This analysis is done by successively simulating altered forms of the system.
This analysis shows that the core system and its altered variants can only provide damped oscillations. In the next section, we examine more significant topology improvements of the core system. |
 "
"