|
Mathematical analysis and simulations
FIFO
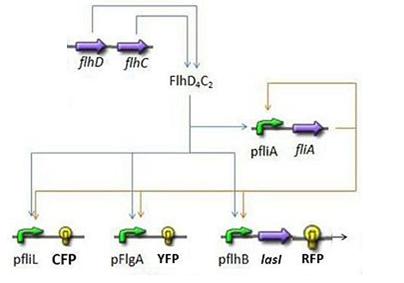
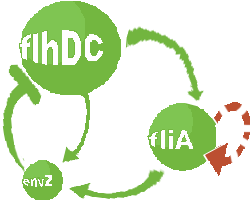
- In order to go further into the details of mathematical analysis of the FIFO, let us remind you the set of equations used and the corresponding network (note that you can have an explanation on the way they have been built on the Model Construction page):
where CFP, YFP, and RFP will be denoted below as respectively Z1,Z2 and Z3.
We have implemented this system using Matlab (see the corresponding codes)
- Then, in order to obtain simulations of the expected FIFO behaviour, we set ideal conditions, by imposing flhDC as a step function, equal to one then to zero.
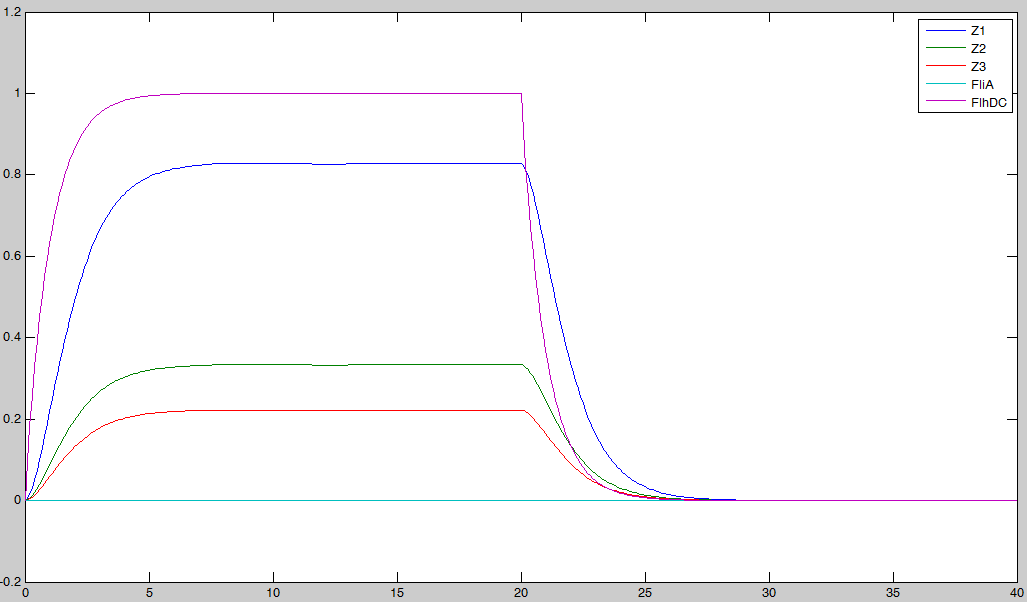
- We saw during the overall description of the core system that without FliA, the FIFO would presumably not work. We then simulated a first system, where [FliA] stays to zero value to confirm that qualitative conclusion :
Indeed, we may see that there is a LIFO behavior rather than the FIFO we expect...
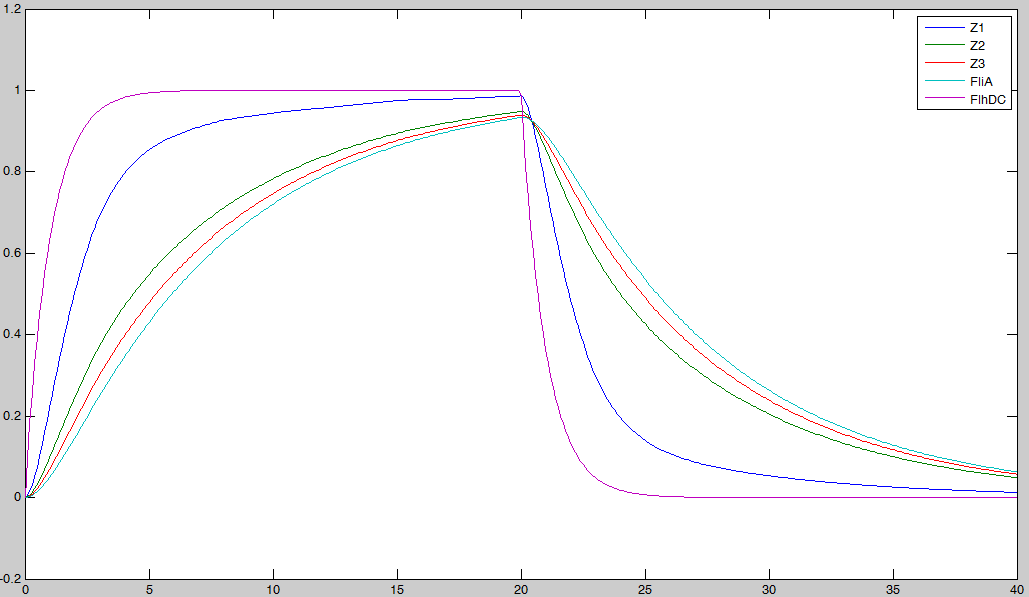
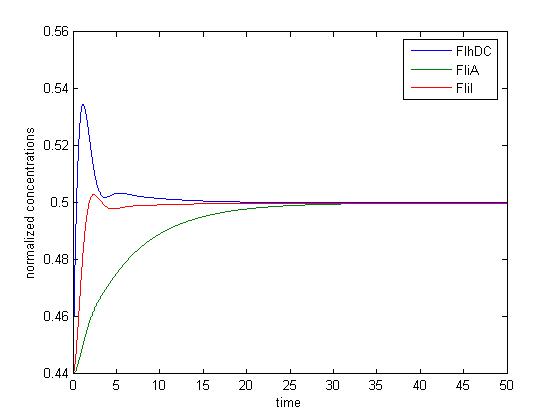
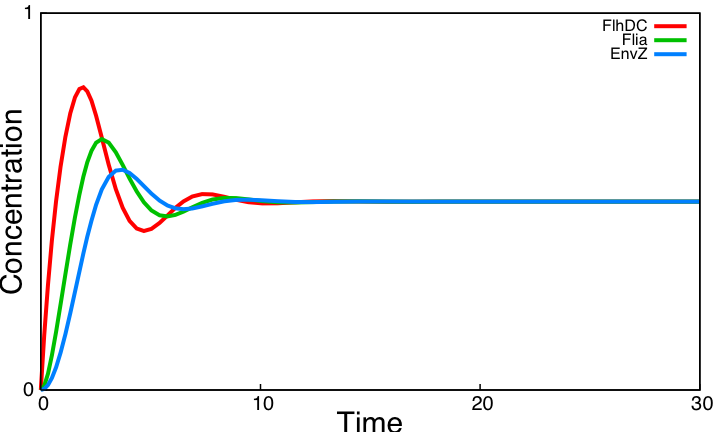
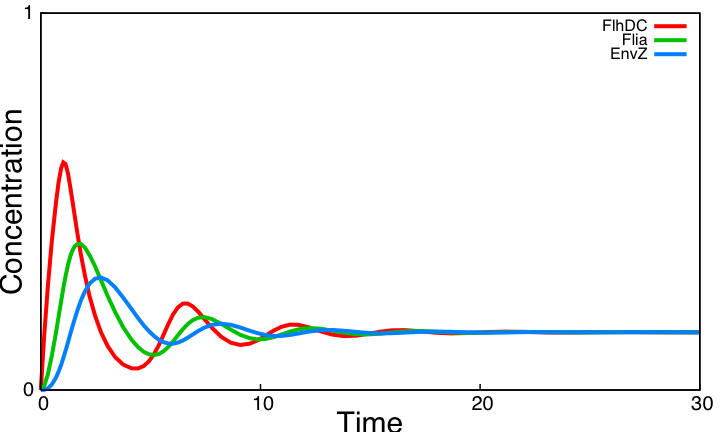
- Then, we simulated the entire system (that means with FliA), to check if we had
- the lasting burst due to FliA (more important for Z3 than for Z2, and more important for Z2 than Z1) in the increasing phase.
- the effect of fliA which maintained the concentrations to their maximum (more important for Z3 than for Z2, and more important for Z2 than Z1) in the decreasing phase. We have obtained the following curves, which are in perfect agreement with the theoretical definition of a 'FIFO' process :
- FliA enables the curves to cross, and adds a delay on the genes that are most affected, with gives a better observability of the FIFO behavior.
Oscillations
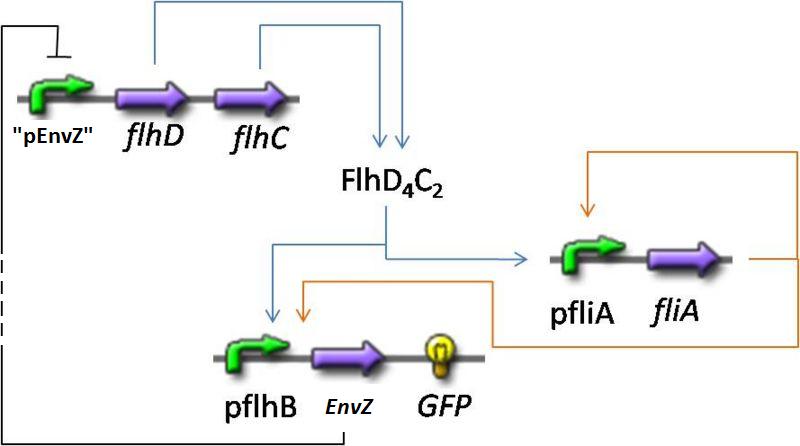
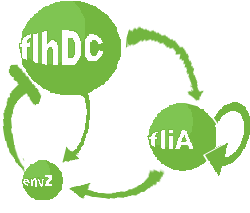
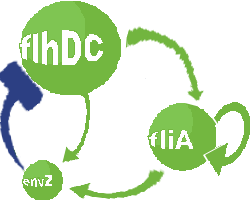
- In addition to the previous FIFO system, we will add a negative feedback on FlhDC promoter to observe oscillations. Thus, we obtained the following network and the corresponding equations (notice that we decide to model in a single arrowthe process through which that EnvZ repress FlhDC):
If you want more details about the way we have built them, you can go to the model construction page.
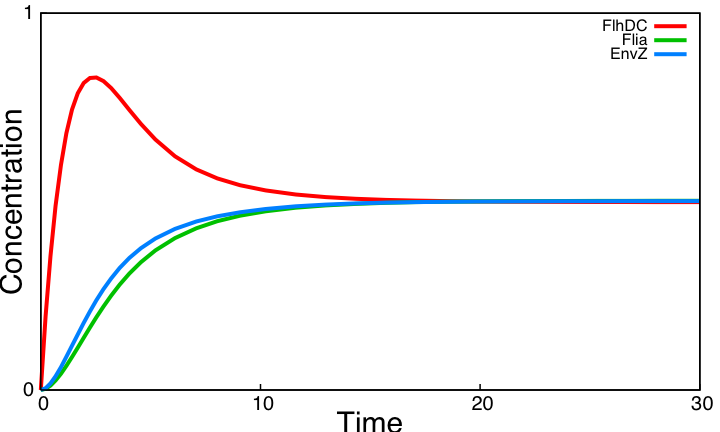
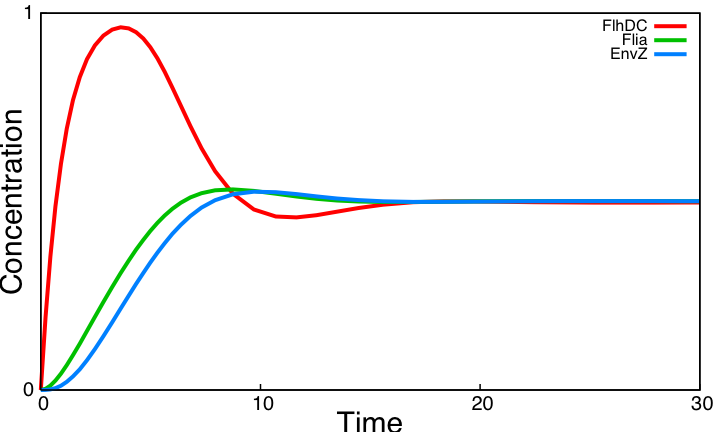
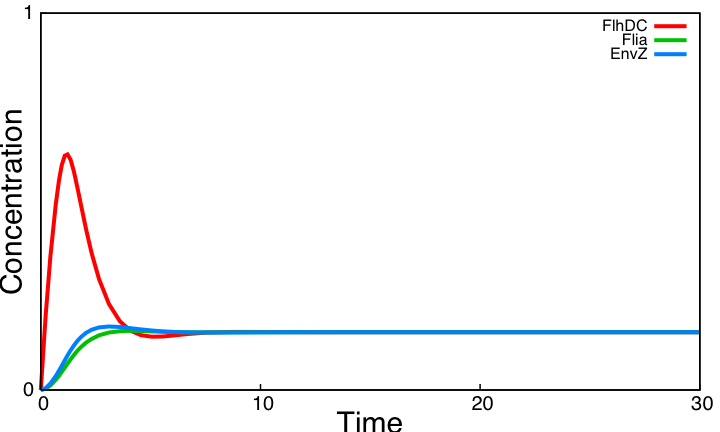
If one tries to draw simulations of this system, he will obtain this kind of results :
In a nutshell : It does not work !
Nonetheless, there are two questions we could focus on:
Finally, the logical continuation of the process will be to try to improve the biological system in order to find oscillations. This will be described in the part below, as well as in the section System Improvements.
System analysis
Simulations of the core system displayed above reveal that it does not exhibit an oscillatory behavior. In this section we use the model of the core system to try to figure out the contribution of some key characteristics of the network topology on the dynamic of the system. This analysis is done by successively simulating altered forms of the system.
The following table lists the different forms of the system considered and their respective outcome :
| Description
| Simulation
| Evaluation
| Interpretation
|
| Core system (without modifications).
|
| 
| Non oscillating system.
|
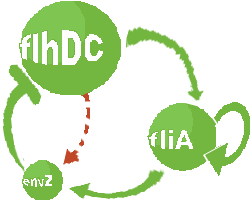
| Removing the activation of envZ via FlhDC.
|
| 
| Non oscillating system. Activation of envZ via FlhDC has a negative effect on the presence of oscillations. This interaction creates a 'shortcut' in the loop, diminishing the effect of Flia in the system. This interaction is already low in the core system, its deletion thus has a moderate positive effect.
|
| Removing the auto-activation of flia
|
|  
| Damped oscillations. Auto-activation of Flia slows its dynamic. For oscillations to appear, different species need to have comparable time scales : oscillations are much more easier without Flia auto-activation.
|
| Enhancing the inhibition of FlhDC via envZ
|
| 
| Non oscillating system. A stronger inhibition slightly improves the behavior of the system.
|
| Combining three modifications all together.
|
|   
| Damped oscillations with greater amplitude. Combining the three previous variants provides the best possible behavior.
|
The core system can only provide damped oscillations. In particular, auto-activation of flia and activation of envZ by FlhDC both have serious negative effects on oscillations. But these actions are required for the FIFO behavior of the system.
In the next section, we examine significant topology improvements of the core system that are potentially better for oscillations and that preserve FIFO required interactions.
Navigator
Back to the overall presentation of our system and model
Top of the page
Mathematical analysis Effects of integration methods
|
 "
"