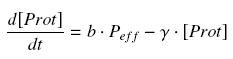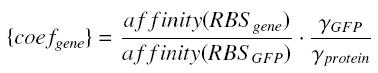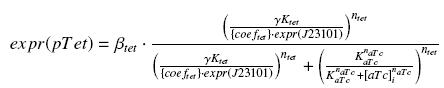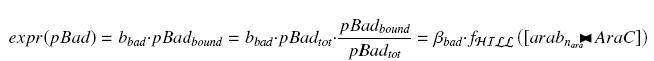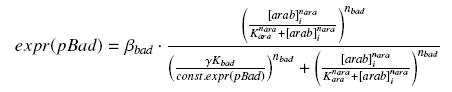Team:Paris/Modeling/estimation
From 2008.igem.org
(→First hypothesis) |
|||
| (42 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| - | {{Paris/ | + | {{:Team:Paris/MenuBackup}} |
=Parameters Estimation= | =Parameters Estimation= | ||
| Line 19: | Line 19: | ||
'''(2)''' We assume that, whatever is the gene behind the promoter, its expression depends only of the transcription factor of the promoter, and not, for instance, of the weight of this gene. That's why comparing promoter strength is relevent only if the genes behind have similar length. | '''(2)''' We assume that, whatever is the gene behind the promoter, its expression depends only of the transcription factor of the promoter, and not, for instance, of the weight of this gene. That's why comparing promoter strength is relevent only if the genes behind have similar length. | ||
| - | '''(3)''' We consider that the activity of a promoter is well described as a a '''transduction rate''' ( ''' ''b'' ''', we will later note ''' ''β'' ''' = ''b*p<sub>tot</sub>'', where ''p<sub>tot</sub>'' denotes the total number of promoters '' | + | '''(3)''' We consider that the activity of a promoter is well described as a a '''transduction rate''' ( ''' ''b'' ''', we will later note ''' ''β'' ''' = ''b*p<sub>tot</sub>'', where ''p<sub>tot</sub>'' denotes the total number of promoters ''p'' present in the cell), multiplied by the amount of '''efficient promoters''' (''p<sub>eff</sub>''), depending on the quantity of its '''transcription factor''' (''TF''), and on the coefficients of their [[Team:Paris/Modeling/Programs#Complexations_Caracterisation|complexation reaction]] (''' ''K'' ''' et ''' ''n'' '''), typically leading to a [[Team:Paris/Modeling/Programs#Hill_Functions|Hill function]]. |
Thus, we suppose that the protein concentration (''Prot'') follows this equation : | Thus, we suppose that the protein concentration (''Prot'') follows this equation : | ||
<center> [[Image:dProt.jpg|center]] </center> | <center> [[Image:dProt.jpg|center]] </center> | ||
| - | where | + | where ''γ'' is a constant, due to degradation and of dilution of the protein, along time and cell divisions. |
Therefore, if we consider a '''steady-state''', for given concentration of the transcription factor, we will have : <center> [[Image:steadystate.jpg|center]] </center> | Therefore, if we consider a '''steady-state''', for given concentration of the transcription factor, we will have : <center> [[Image:steadystate.jpg|center]] </center> | ||
| - | '''(4)''' Endly, knowing | + | '''(4)''' Endly, knowing ''γ'' will give us the data we are looking for. In a first approach, we assume that, as long as the barcteria are in their '''phase of exponential growth''', the degradation is far smaller than the dilution, and can be omitted. But we will probably discuss that later (see [[Team:Paris/Modeling/estimation#The_Problem_of_the_RBS|considerations on RBS]]). |
First, we wanted to keep a permanent exponential phase of growth with the system of Ron Weiss (see [[Team:Paris/Project|our project]]), but we finally (to simplify our already huge construction!) decided to put the cells-culture in a '''chemostat''' (see [[Team:Paris/Modeling/hill_approach#Bio-Chemical_General_Assumptions|Bio-Chemical General Assumptions]]). | First, we wanted to keep a permanent exponential phase of growth with the system of Ron Weiss (see [[Team:Paris/Project|our project]]), but we finally (to simplify our already huge construction!) decided to put the cells-culture in a '''chemostat''' (see [[Team:Paris/Modeling/hill_approach#Bio-Chemical_General_Assumptions|Bio-Chemical General Assumptions]]). | ||
| Line 31: | Line 31: | ||
<br>Actually, we will use the linear relation between GFP mut3B concentration (nM) and fluorescence (au), given in the registry [[Team:Paris/Modeling/Bibliography|[6]]]. The conversion factor is 79,429. | <br>Actually, we will use the linear relation between GFP mut3B concentration (nM) and fluorescence (au), given in the registry [[Team:Paris/Modeling/Bibliography|[6]]]. The conversion factor is 79,429. | ||
| - | |||
| - | |||
| - | |||
| - | + | ==RBS Issue== | |
| + | The promoter is not the only one factor which control the expression of the protein... in particular, the ''traduction phenomenon'' is almost as important as the ''transduction''. As we decided not to take into acount the traduction, that means that we do not want to deal with mRNA and ribosomes ; nevertheless, as we aimed in the "APE approach" to simulate as precisely as possible the involved concentrations, we must ''integrate in the traduction simulation the most important influences of the transduction''. | ||
| - | + | Therefore, rigorously, we must describe an induction (or repression) by the association "promoter + specific RBS". | |
| - | + | Still, as it is proposed by iGEM, we will use the GFPgenerator (E0240) in association with its RBS (E0032), to caracterise the '''expression of the gene behind a given promoters'''. However, the RBS before the genes which codes for the ''transcriptions factors'' we want to induce, are the natural RBS (specific respectively to ''tetR'', ''flhDC'', ''fliA'', etc... ). Therefore, we must pay attention on what we are measuring. | |
| - | + | The idea is that, by considering that the ''traduction rate'' depends near '''linearly of the Ribosome Binding Site''' (as we guess ; it gives the affinity between the mRNA and the ribosome !), we introduce a constant factor between the ''expected'' value of a protein and its ''real'' value. | |
| - | + | Moreover, we observe that at the steady state, the degradation rate ''γ'' has got a linear effect on the concentration of the protein at equilibrium, too. | |
| - | + | For instance, if we consider a protein ''prot'' coded by its corresponding ''gene'', put behind one of our "caracterised promoters", with its natural RBS, we will have between our construction (''expected'' value, given by GFP) and the ''real'' expression of ''prot'' the following relation | |
| - | + | [[Image:protcoef.jpg|center]] where [[Image:coef.jpg|center]] | |
| - | + | Because we want to stay as near as possible to the "natural construction of the flagella" (see [[Team:Paris/Project|our project]]), we will keep the natural RBS of every genes we want to put in our final construction (particularly ''flhDC'' and ''fliA''). | |
| - | + | Because of the undetermined strength of the RBS and degradation rate of the different proteins, the parameters we will have acces to are biased. When a parameter is noted K<sub>ref</sub> and is referenced later in K<sub>ref</sub>/{coef}, | |
| - | + | that means that we will calculate the latter, and that this value will be the one instead of the former in the [[Team:Paris/Modeling/FIFO#Resulting_Equations|equations]] we will introduce in the system of ODE. | |
| - | + | Also we must remember that the we are not necessarly dealing with real quantities, but with ''abstract quantities that are coherents together, in our construction''. Finally, in our research of caraterising the expression of the genes in a so simplified way, those methods allow us to skip evaluations of the relative strength of the RBS, and of the degradation rates of our proteins. | |
| - | + | To conclude, we nevertheless must notice that the effect of the coefficient ''γ'' in our model has got an other effect : it changes the dynamics of the system, in the time in which the ''steady states'' are reached. As our system intend to produce ''oscillations'', the ''transcient states'' are important, and here is the biggest weakness of this model. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ==How to control the concentration of the transcription factor ?== | |
| - | + | ===Using {aTc, TetR, pTet}=== | |
| + | Now, we must use as a variable of reference an element that could be introduced in the bacteria, well-controlled, and from which all the concentrations of our transcription factor will depend. We propose a construction in which our transcription factor is put after the promoter pTet, which is under the repression of TetR. Since aTc is a small diffusive molecule that binds to TetR and inhibits this way the repression of pTet, we can use it as an "inducer". To do so, we must place in the bacterium the gene ''tetR'' after a constitutive promoter (like J23101). | ||
| - | + | We have | |
| - | + | ||
| - | + | [[Image:ExprTetR.jpg|center]] | |
| - | + | So, according to the calculus on [[Team:Paris/Modeling/Programs#Induction_for_the_caracterisations|the diffusion and complexation]] we will get at the steady-state : | |
| - | |||
| - | + | [[Image:ExprTetREq.jpg|center]] | |
| - | |||
| - | [[ | + | In the last equation, we will have 'access' (see [[Team:Paris/Modeling/estimation#First_hypothesis|hypothesis '''(5)''']]) to ''expr(pTet)'' and possibly to ''γ'', and we are looking for β<sub>tet</sub>, K<sub>tet</sub> and n<sub>tet</sub>, thanks to our program (see [[Team:Paris/Modeling/estimation#Getting_a_.22complexation_function.22_from_convenient_datas|getting Hill function with convenient datas]]). |
| + | We control [aTc]<sub>i</sub> and we will caracterise ''expr(J23101)'' (see [[Team:Paris/Modeling/estimation#What_are_we_looking_for_.3F|the functions we are looking for]]). Then, to solve the equation, we need K<sub>aTc</sub> and n<sub>aTc</sub>. | ||
| + | Therefore, we will first brievly look into the literature, and then complexify the [[Team:Paris/Modeling/Programs#Finding_Parameters|'findparam' function]], in order to seek for these two more parameters. This new program allows us to get [[Team:Paris/Modeling/Programs#Induction_by_a_small_molecule|Prot = fun(mol_dif,rec)]], i.e. a protein expression in function of a small diffusive molecule and of its receptor, acting on a specific promoter. | ||
| - | + | ===Using {AraC, Arabinose, pBad}=== | |
| - | + | An other well-known promoter called pBad, is induced by the complex AraC><arab, where AraC appears to be a protein ''constitutively produced'' by an operon attached to pBad, and arabinose is a sugar, that we can add at will in the medium, and diffuses through cells. | |
| + | We have : | ||
| - | + | [[Image:exprpBad.jpg|center]] | |
| - | + | we find at steady state (with obvious notations, as in the last paragraph) | |
| - | + | ||
| - | + | [[Image:PbadArab.jpg|center]] | |
| - | + | ||
| + | However, we do not need any estimation of ''const.expr(pBad)'', because we do not have to get the "real" K<sub>bad</sub>, since we will only use this promoter in ''caracterisation systems''. Then, we will treat the other parameters exactly as for the ''pTet system''. | ||
| + | |||
| + | ==What are we looking for ?== | ||
| + | The different functions we would like to determine are the followings. They are linked to a basic description of the "theoretical protocol" that will allow us to get the expected datas. We decided, as far as possible, to keep the original genome of the bacteria, so that the strength that we are measuring is ''' the strength for an "additional" promoter in the cell''', keeping those which already exist : this makes sense for our construction, and probably for most of the constructions of synthetic biology wih ''E.coli''. | ||
| Line 96: | Line 95: | ||
*[[Team:Paris/Modeling/f1|[expr.(pTet)] = ƒ1([TetR],[aTc])]] | *[[Team:Paris/Modeling/f1|[expr.(pTet)] = ƒ1([TetR],[aTc])]] | ||
| - | *[[Team:Paris/Modeling/f2|[expr.(pBad)] = ƒ2([ | + | *[[Team:Paris/Modeling/f2|[expr.(pBad)] = ƒ2([arabinose])]] |
| - | + | <br> | |
*[[Team:Paris/Modeling/f3|[expr.(pFlhDC)] = ƒ3([OmpR*],[FliA])]] | *[[Team:Paris/Modeling/f3|[expr.(pFlhDC)] = ƒ3([OmpR*],[FliA])]] | ||
| - | *[[Team:Paris/Modeling/ | + | *[[Team:Paris/Modeling/f3bis|[expr.(pFlhDC)] = ƒ3bis([EnvZ],[FliA])]] |
*[[Team:Paris/Modeling/f4|[expr.(pFlhDC)] = ƒ4([FlhDC],[FliA])]] | *[[Team:Paris/Modeling/f4|[expr.(pFlhDC)] = ƒ4([FlhDC],[FliA])]] | ||
| Line 115: | Line 114: | ||
*[[Team:Paris/Modeling/f9|[expr.(pLas)] = ƒ9([LasR><HSL])]] | *[[Team:Paris/Modeling/f9|[expr.(pLas)] = ƒ9([LasR><HSL])]] | ||
| - | |||
| - | |||
= Noise estimation = | = Noise estimation = | ||
| - | Firstly, we could compute the standard deviation for each set of points at a given inducer concentration, and to normalize it according to the mean value of the set itself. | + | Firstly, we could compute the standard-deviation for each set of points at a given inducer concentration, and to normalize it according to the mean value of the set itself. |
| - | The next stage is to get the mean of those normalized | + | The next stage is to get the mean ('''σ''') of those normalized s-d values at every inducer concentration. |
| - | Since the β parameter | + | Since the '''β''' parameter (''production rate'') has a linear influence on a production function, it is possible to translate this error directly on the parameter; for example: '''β<sub>stochastic</sub> ~ LG(β,σ)''', where LG denotes a Laplace-Gauss law of probability. |
For each cell in the model, we could use such noised values for Vmax parameter, in order to reproduce randomness estimated in the wet lab. | For each cell in the model, we could use such noised values for Vmax parameter, in order to reproduce randomness estimated in the wet lab. | ||
Latest revision as of 07:07, 30 October 2008
Go back to the normal Wiki
Contents |
Parameters Estimation
Getting a "complexation function" from convenient datas
Therefore, we have written a little module which can estimate the parameters of a complexation function, even with some noise and few data available.
The method we have employed is essentially based on a least-square optimization.
Getting convenient datas
Thus, we need experimental datas. To quantify the strength of a transcription factor on a promoter, we will use measurements of GFP fluorescence, and compare to the strength of the constitutive promoter http://partsregistry.org/Measurement/SPU/Learn J23101, as it was proposed by the iGEM competition. The datas we are looking for must appear as a table of values, giving several "expression rates" with their corresponding "transcription factor concentrations".
First hypothesis
For this aim, we made several hypothesis, which we will verify as good as it is possible for us :
(1) We do not take into acount the 'traduction' phase (see however considerations on RBS), so we directly correlate the transcription of a gene with the concentration of its protein.
(2) We assume that, whatever is the gene behind the promoter, its expression depends only of the transcription factor of the promoter, and not, for instance, of the weight of this gene. That's why comparing promoter strength is relevent only if the genes behind have similar length.
(3) We consider that the activity of a promoter is well described as a a transduction rate ( b , we will later note β = b*ptot, where ptot denotes the total number of promoters p present in the cell), multiplied by the amount of efficient promoters (peff), depending on the quantity of its transcription factor (TF), and on the coefficients of their complexation reaction ( K et n ), typically leading to a Hill function. Thus, we suppose that the protein concentration (Prot) follows this equation :
where γ is a constant, due to degradation and of dilution of the protein, along time and cell divisions.
Therefore, if we consider a steady-state, for given concentration of the transcription factor, we will have :(4) Endly, knowing γ will give us the data we are looking for. In a first approach, we assume that, as long as the barcteria are in their phase of exponential growth, the degradation is far smaller than the dilution, and can be omitted. But we will probably discuss that later (see considerations on RBS). First, we wanted to keep a permanent exponential phase of growth with the system of Ron Weiss (see our project), but we finally (to simplify our already huge construction!) decided to put the cells-culture in a chemostat (see Bio-Chemical General Assumptions).
(5) Unless we find further documents dealing with the relation between the intensity of fluorescence and the concentration of GFP, we will directly use the measure in fluorescence, that we will treat as a protein concentration, more or less arbitrary normalised.
Actually, we will use the linear relation between GFP mut3B concentration (nM) and fluorescence (au), given in the registry [6]. The conversion factor is 79,429.
RBS Issue
The promoter is not the only one factor which control the expression of the protein... in particular, the traduction phenomenon is almost as important as the transduction. As we decided not to take into acount the traduction, that means that we do not want to deal with mRNA and ribosomes ; nevertheless, as we aimed in the "APE approach" to simulate as precisely as possible the involved concentrations, we must integrate in the traduction simulation the most important influences of the transduction.
Therefore, rigorously, we must describe an induction (or repression) by the association "promoter + specific RBS".
Still, as it is proposed by iGEM, we will use the GFPgenerator (E0240) in association with its RBS (E0032), to caracterise the expression of the gene behind a given promoters. However, the RBS before the genes which codes for the transcriptions factors we want to induce, are the natural RBS (specific respectively to tetR, flhDC, fliA, etc... ). Therefore, we must pay attention on what we are measuring.
The idea is that, by considering that the traduction rate depends near linearly of the Ribosome Binding Site (as we guess ; it gives the affinity between the mRNA and the ribosome !), we introduce a constant factor between the expected value of a protein and its real value.
Moreover, we observe that at the steady state, the degradation rate γ has got a linear effect on the concentration of the protein at equilibrium, too.
For instance, if we consider a protein prot coded by its corresponding gene, put behind one of our "caracterised promoters", with its natural RBS, we will have between our construction (expected value, given by GFP) and the real expression of prot the following relation
whereBecause we want to stay as near as possible to the "natural construction of the flagella" (see our project), we will keep the natural RBS of every genes we want to put in our final construction (particularly flhDC and fliA).
Because of the undetermined strength of the RBS and degradation rate of the different proteins, the parameters we will have acces to are biased. When a parameter is noted Kref and is referenced later in Kref/{coef}, that means that we will calculate the latter, and that this value will be the one instead of the former in the equations we will introduce in the system of ODE.
Also we must remember that the we are not necessarly dealing with real quantities, but with abstract quantities that are coherents together, in our construction. Finally, in our research of caraterising the expression of the genes in a so simplified way, those methods allow us to skip evaluations of the relative strength of the RBS, and of the degradation rates of our proteins.
To conclude, we nevertheless must notice that the effect of the coefficient γ in our model has got an other effect : it changes the dynamics of the system, in the time in which the steady states are reached. As our system intend to produce oscillations, the transcient states are important, and here is the biggest weakness of this model.
How to control the concentration of the transcription factor ?
Using {aTc, TetR, pTet}
Now, we must use as a variable of reference an element that could be introduced in the bacteria, well-controlled, and from which all the concentrations of our transcription factor will depend. We propose a construction in which our transcription factor is put after the promoter pTet, which is under the repression of TetR. Since aTc is a small diffusive molecule that binds to TetR and inhibits this way the repression of pTet, we can use it as an "inducer". To do so, we must place in the bacterium the gene tetR after a constitutive promoter (like J23101).
We have
So, according to the calculus on the diffusion and complexation we will get at the steady-state :
In the last equation, we will have 'access' (see hypothesis (5)) to expr(pTet) and possibly to γ, and we are looking for βtet, Ktet and ntet, thanks to our program (see getting Hill function with convenient datas).
We control [aTc]i and we will caracterise expr(J23101) (see the functions we are looking for). Then, to solve the equation, we need KaTc and naTc.
Therefore, we will first brievly look into the literature, and then complexify the 'findparam' function, in order to seek for these two more parameters. This new program allows us to get Prot = fun(mol_dif,rec), i.e. a protein expression in function of a small diffusive molecule and of its receptor, acting on a specific promoter.
Using {AraC, Arabinose, pBad}
An other well-known promoter called pBad, is induced by the complex AraC><arab, where AraC appears to be a protein constitutively produced by an operon attached to pBad, and arabinose is a sugar, that we can add at will in the medium, and diffuses through cells. We have :
we find at steady state (with obvious notations, as in the last paragraph)
However, we do not need any estimation of const.expr(pBad), because we do not have to get the "real" Kbad, since we will only use this promoter in caracterisation systems. Then, we will treat the other parameters exactly as for the pTet system.
What are we looking for ?
The different functions we would like to determine are the followings. They are linked to a basic description of the "theoretical protocol" that will allow us to get the expected datas. We decided, as far as possible, to keep the original genome of the bacteria, so that the strength that we are measuring is the strength for an "additional" promoter in the cell, keeping those which already exist : this makes sense for our construction, and probably for most of the constructions of synthetic biology wih E.coli.
Noise estimation
Firstly, we could compute the standard-deviation for each set of points at a given inducer concentration, and to normalize it according to the mean value of the set itself.
The next stage is to get the mean (σ) of those normalized s-d values at every inducer concentration.
Since the β parameter (production rate) has a linear influence on a production function, it is possible to translate this error directly on the parameter; for example: βstochastic ~ LG(β,σ), where LG denotes a Laplace-Gauss law of probability.
For each cell in the model, we could use such noised values for Vmax parameter, in order to reproduce randomness estimated in the wet lab.
 "
"