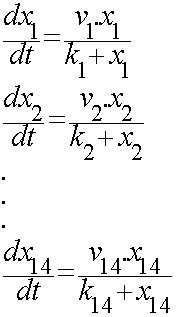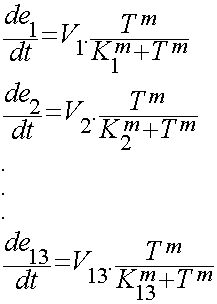Team:TUDelft/Color modeling
From 2008.igem.org
(→Color Modeling) |
(→Color Modeling) |
||
| Line 13: | Line 13: | ||
<center> <b> Color Pathway </b> </center> | <center> <b> Color Pathway </b> </center> | ||
| + | ==Differential Equations== | ||
For the 14 reactions of enzyme-substrate the Michaelis-Menten kinetics is applied and we have the mass action kinetics for the three degradations. | For the 14 reactions of enzyme-substrate the Michaelis-Menten kinetics is applied and we have the mass action kinetics for the three degradations. | ||
| - | According to the kinetic laws there are 14 differential equations for enzyme- | + | According to the kinetic laws there are 14 differential equations for enzyme-substrate reactions and three for degradations which could be constructed as: |
| - | [[Image:Eq1.gif |120px]] | + | [[Image:Eq1.gif |120px | center]] |
x<sub>1</sub> to x<sub>14</sub> are the subtrates. | x<sub>1</sub> to x<sub>14</sub> are the subtrates. | ||
| - | [[Image:Enz1.gif | | + | [[Image:Enz1.gif |140px | center]] |
| - | We used hill type model for enzyme temperature relations where e<sub>1</sub> to e<sub>13</sub> are the enzymes. | + | We used hill type model for enzyme temperature relations where e<sub>1</sub> to e<sub>13</sub> are the enzymes. Afterwards the in '''CellDesigner™''' file was imported into Matlab. For this procedure many softwares were tested but finally the [ ] site used to convert the SBML model into m file. This m file was the base part for the modeling in Matlab. In this m file all the related differential equations were defined as a function with the time span and initial condition as the input. The reactions coefficients are defined by some not systemically acquired numbers to give an estimation for the reactions. These differential equations were solved by Matlab ODE function. |
The next step is to find the coefficients of V and K for the both set of equations. | The next step is to find the coefficients of V and K for the both set of equations. | ||
Revision as of 10:35, 16 September 2008
>> work in progress
Color Modeling
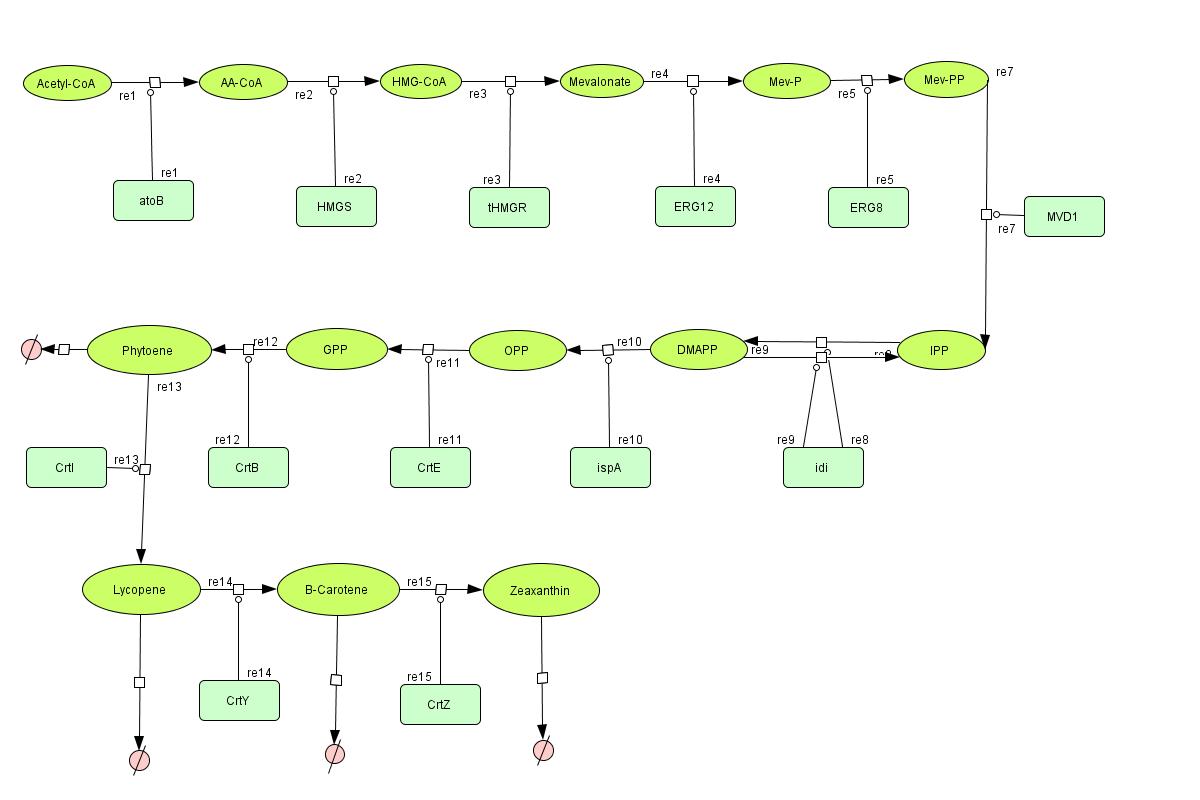
In the output we use [http://www.lbl.gov/Science-Articles/Archive/assets/images/2004/Mar-24/Engineering_terpenoids.pdf mevalonate] and [http://parts.mit.edu/igem07/index.php/Image:Zeaxanthin.jpg GPP] pathways together to produce red, orange and yellow colors. The biosynthetic model is built in CellDesigner™. There are 14 substrates and 13 enzymes in total. The first substrate is Acetyl-CoA which is provided to the pathway in a constant level. The last three substrates are the color products and are consuming so we have degradation links for them. Lycopene, B-carotene and Zeaxanthin give red, orange and yellow colors respectively.
Differential Equations
For the 14 reactions of enzyme-substrate the Michaelis-Menten kinetics is applied and we have the mass action kinetics for the three degradations. According to the kinetic laws there are 14 differential equations for enzyme-substrate reactions and three for degradations which could be constructed as:
x1 to x14 are the subtrates.
We used hill type model for enzyme temperature relations where e1 to e13 are the enzymes. Afterwards the in CellDesigner™ file was imported into Matlab. For this procedure many softwares were tested but finally the [ ] site used to convert the SBML model into m file. This m file was the base part for the modeling in Matlab. In this m file all the related differential equations were defined as a function with the time span and initial condition as the input. The reactions coefficients are defined by some not systemically acquired numbers to give an estimation for the reactions. These differential equations were solved by Matlab ODE function.
The next step is to find the coefficients of V and K for the both set of equations. In the subtrate equations we have Vmax=Kcat . E0 where Kcat is the turnover number and E0 is the enzyme's initial concentration.
... to be continued
 "
"