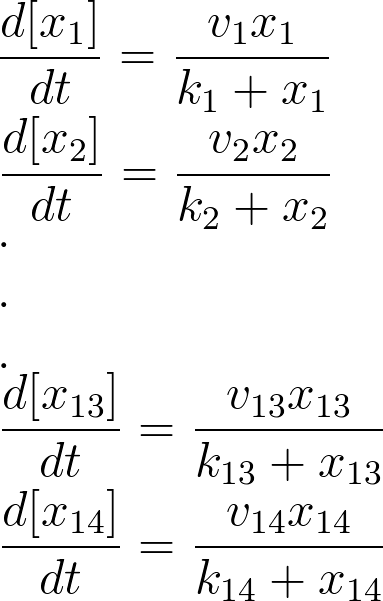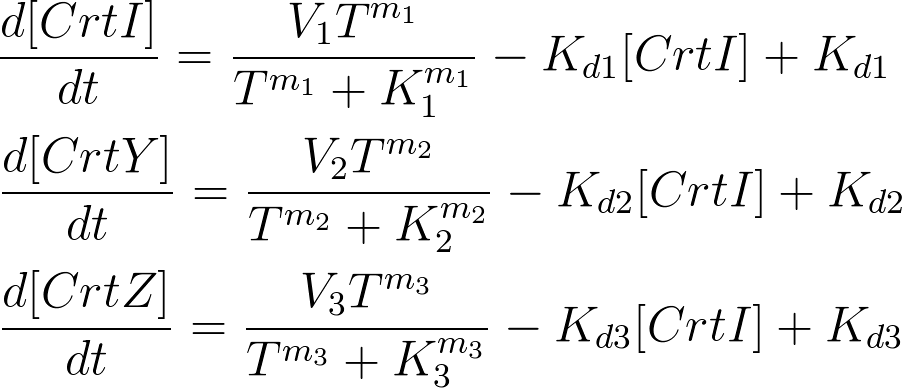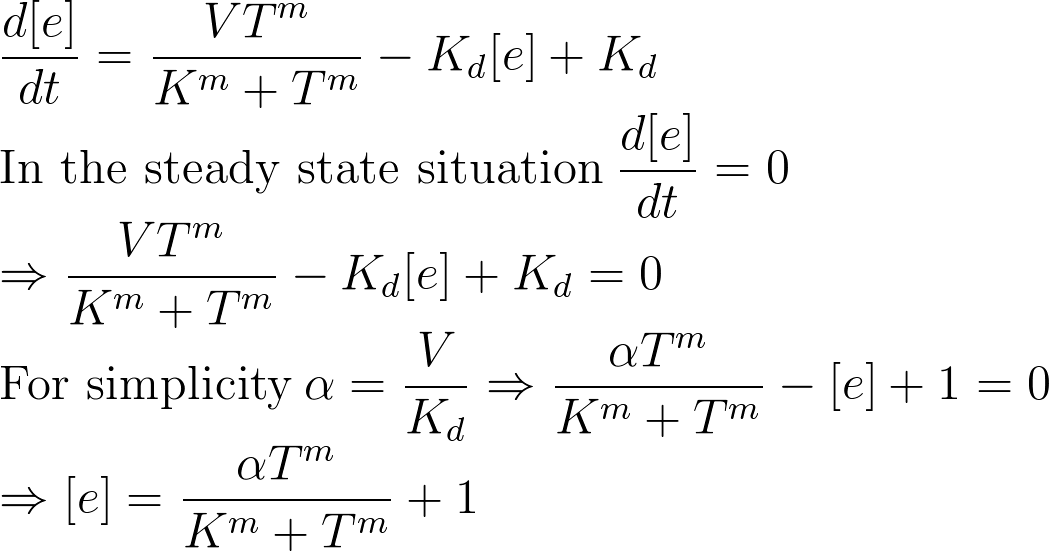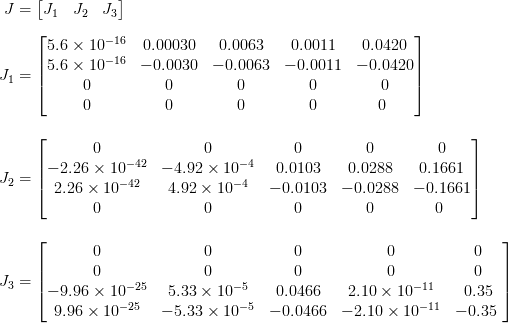Team:TUDelft/Color modeling
From 2008.igem.org
Contents |
Introduction
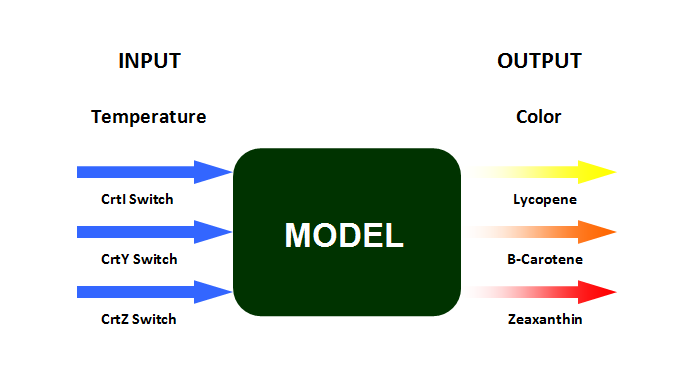
The model of the biothermometer includes three inputs and three outputs. The input of the model is the enzyme synthesis controlled by the temperature and the output is color production. The challenges for the modeling part are:
- Finding a suitable model for a temperature dependence synthesis of the color producing enzymes.
- Solving the Michaelis-Menten kinetic equations to obtain the dynamics of pathway intermediates.
The procedure for modeling was started with the output part, color pathway, and continued to the enzyme synthesis which can be controlled by temperature.
The Output
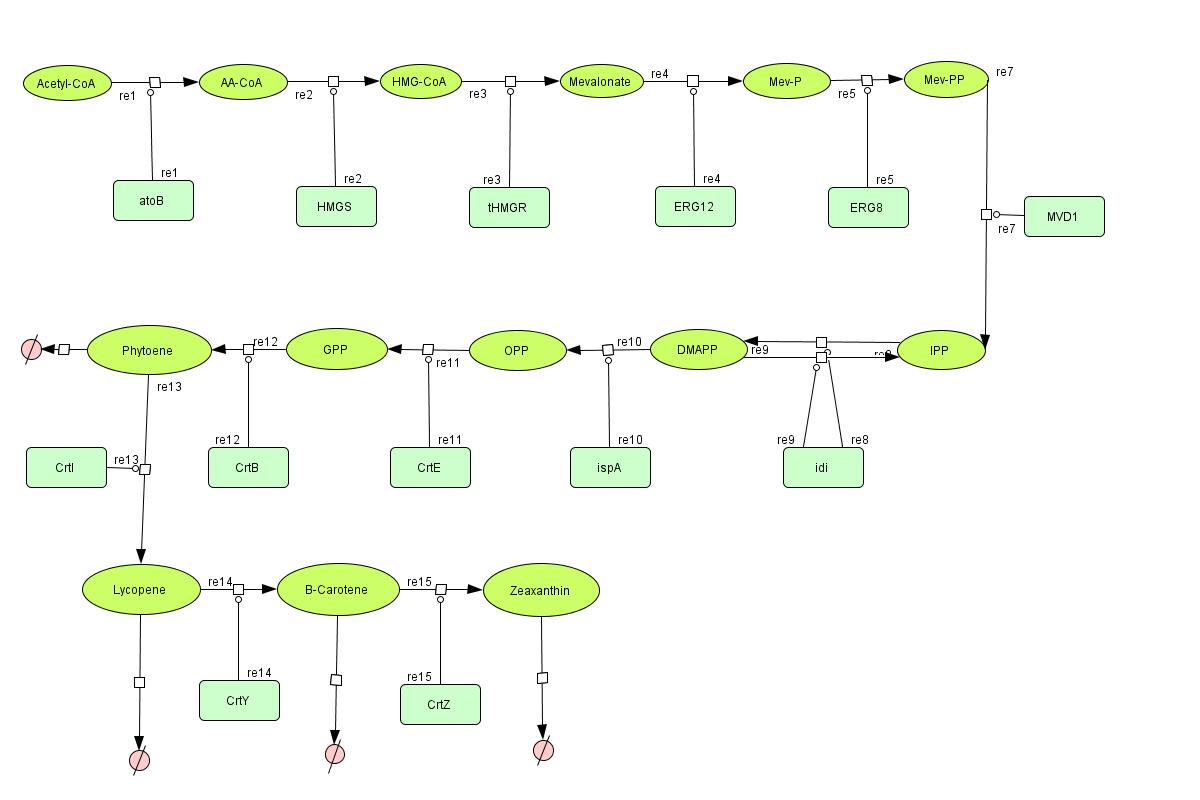
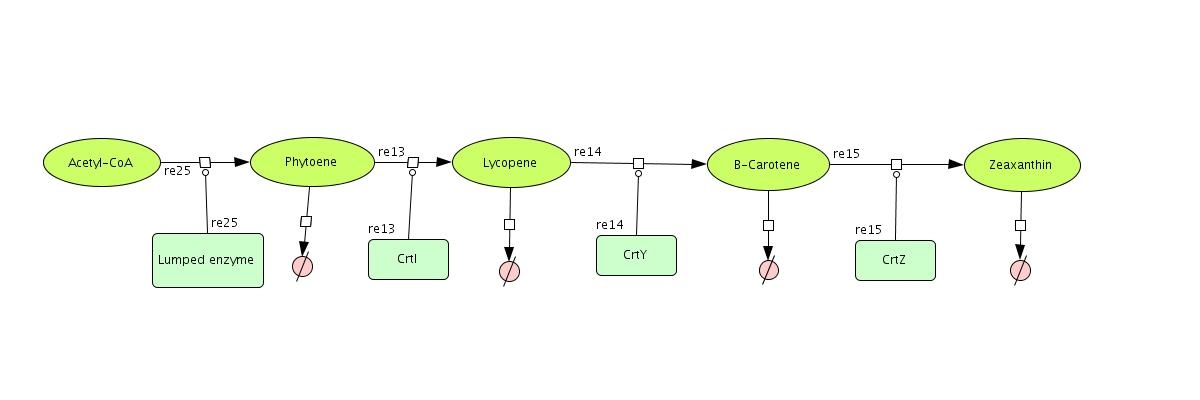
In the output we use [http://www.lbl.gov/Science-Articles/Archive/assets/images/2004/Mar-24/Engineering_terpenoids.pdf mevalonate] and GPP pathways together to produce red, orange and yellow colors. The biosynthetic model is built in CellDesigner™. There are 14 substrates and 14 enzymes in total (idi counts twice as it acts on two reactions). The first substrate is Acetyl-CoA which is provided to the pathway in a constant level. The last three substrates are the color products and are consuming so we have degradation links for them. If we turn off the first switch (CrtI) then there will be no production of Lycopene and Phytoene will be degraded in time, so there is another degradation link in the model for the Phytoene . At last Lycopene, B-carotene and Zeaxanthin give red, orange and yellow colors respectively.
Kinetic Equations
For the 14 reactions of enzyme-substrate the Michaelis-Menten kinetics is applied and we have the mass action kinetics for the four degradations. According to the kinetic laws there are 14 differential equations for enzyme-substrate reactions and four for degradations which could be constructed as:
The [http://www.sys-bio.org synthetic biology workbench] was used to convert the SBML model in CellDesigner™ into an M-file in Matlab®. This M-file was the basic part of the code for modeling in Matlab®. In the M-file all the related differential equations are defined as functions with the time spans and initial conditions as the inputs.
The K coefficients for our pathway and organism were not available from databases. From the work of [http://www.molgen.mpg.de/~lieberme/data/ibsb2007_Borger_et_al.pdf Borger et al. 2007] we expected that K has a Gaussian distribution so we took the minimum and maximum possible values of K from [http://www.brenda-enzymes.info/ Brenda] and made a normal distribution of them. Now the value for K is picked randomly from this distribution.
After the conversion of SBML model to the M-file, the code needed some modifications. The modified code gave the right set of differential equations which were solved by Matlab® ODE solver. The codes that used in this part are available through the Downloads tab.
System of ODEs
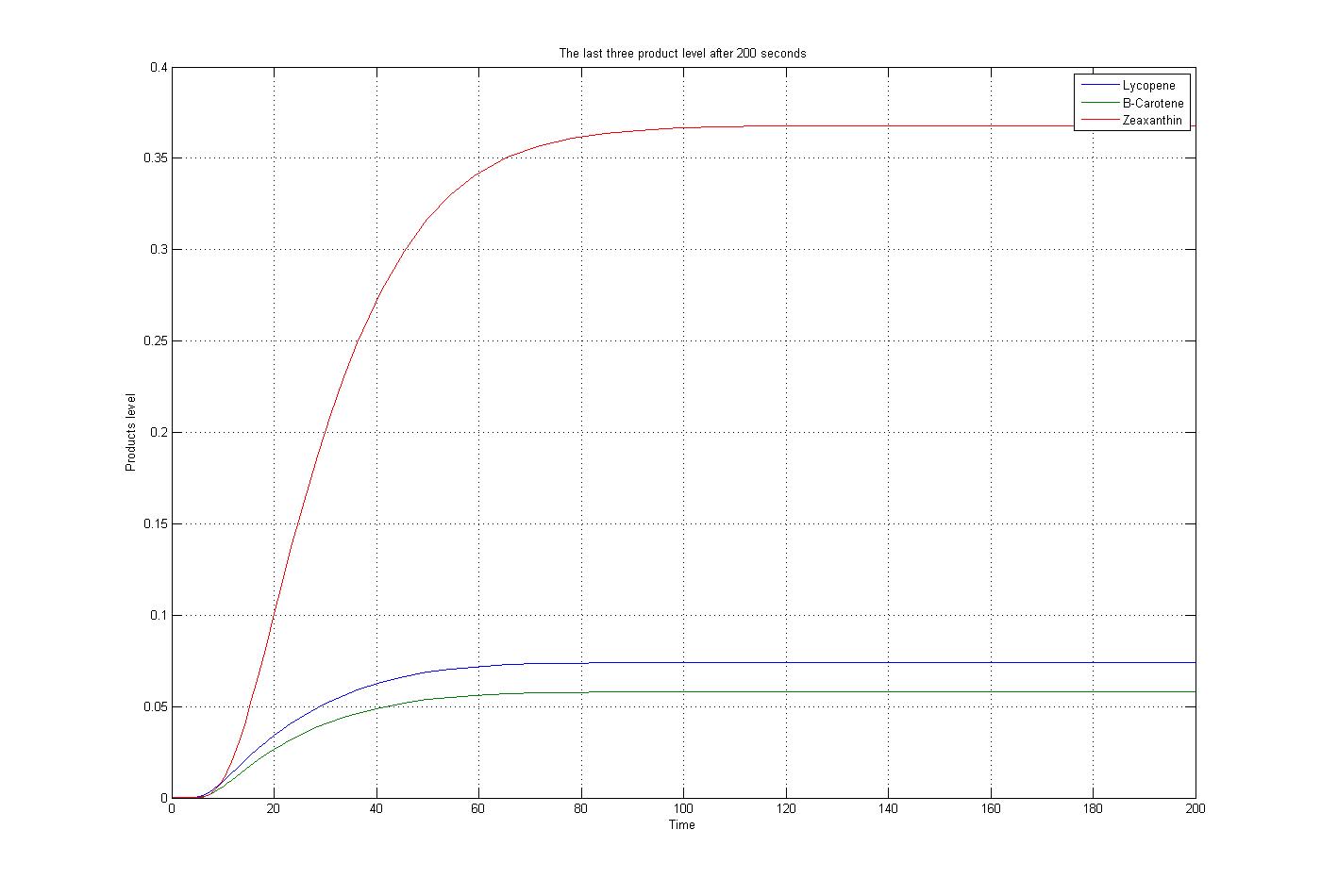
The M-file function, as mentioned before, was solved by the ode15s function of Matlab. To do this procedure some assumptions were applied. The first substrate, Acetyl-CoA, was assumed to be produced and consumed with the same rate. Also for simplification the level of enzymes was assumed to be constant. The reaction coefficients are defined the same for all reactions with some estimated numbers to give an overview about the reactions. The results for these assumptions, specific boundary condition and a time span of 200 seconds were plotted. These results show the steady state situation for the last three products after 200 seconds. The plot is:
Effects of the temperature on enzymes
[http://student.ccbcmd.edu/biotutorials/proteins/enzyme.html Enzymes] are catalysts that breakdown or synthesize more complex chemical compounds. They allow chemical reactions to occur fast enough to support life. Anything that an enzyme normally combines with is called a substrate. Each enzyme has an [http://student.ccbcmd.edu/biotutorials/proteins/enzyme.html optimum temperature] at which it works best. A higher temperature generally results in an increase in enzyme activity. As the temperature increases, molecular motion increases resulting in more molecular collisions. If, however, the temperature rises above a certain point, the heat will denature the enzyme, causing it to lose its three-dimensional functional shape by denaturing its hydrogen bonds. Cold temperature, on the other hand, slows down enzyme activity by decreasing molecular motion. In the monitored model the effect of temperature is important for the last three enzymes. Moreover the last three enzymes are produced on specific temperatures to active the last three product reactions. These last three products are [http://en.wikipedia.org/wiki/Lycopene Lycopene], [http://en.wikipedia.org/wiki/Beta-carotene B-Carotene] and [http://en.wikipedia.org/wiki/Zeaxanthin Zeaxanthin] which represent red, orange and yellow color in the environment.
For the enzymes production the hill type model was used. As a result, the temperature is the main parameter in enzyme production rate. Due to degradation, which is dependent on the enzyme concentration, after a while the enzyme concentration is in a stable situation. Moreover, with the hill type model the enzymes work as a switch which are activated on a certain temperature. The activation temperature is determined by the parameters in the hill type equation.
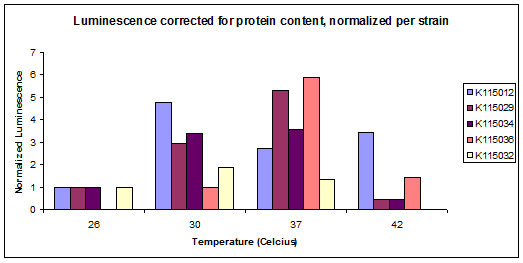
Experimental Data from the Lab
In the model, there are many parameters that were estimated arbitrarily to have an initial calculation and get a feeling about the model. However to have a good model it is necessary to have a good estimation for the parameters. To find these estimation the modeling crew decided to use the results from the lab. It means that the results from lab were used to estimate parameters that were not available exactly in databases. Two experiments have been designed for this procedure. The first one was an experiment for steady state situation which has been done by using luciferase. In this experiment the enzyme activity has been measured for a specific temperature in the steady state situation. As this experiment has been done in steady state situation it was named "static". The second experiment was designed to measure enzyme activity in a changing situation. It means that the enzyme activities were measured in a changing temperature in different time spans. As this experiment is performed in a changing situation it was named "dynamic". The results of both experiments are used to help the modeling crew to find a good estimation for parameters. An example for the lab experiment results in the steady state, which has been normalized, is shown below. These results have been used to do the calculations for the next steps.
Parameter Estimation
In the first step, the results from steady state situation were used to calculate the parameters. In steady state situation the enzyme concentration ratio is zero. Therefore from the lab results it is possible to derive a equation that has enzyme concentration. In this equation the enzyme concentration and temperature are known and alpha, m and K are unknown.
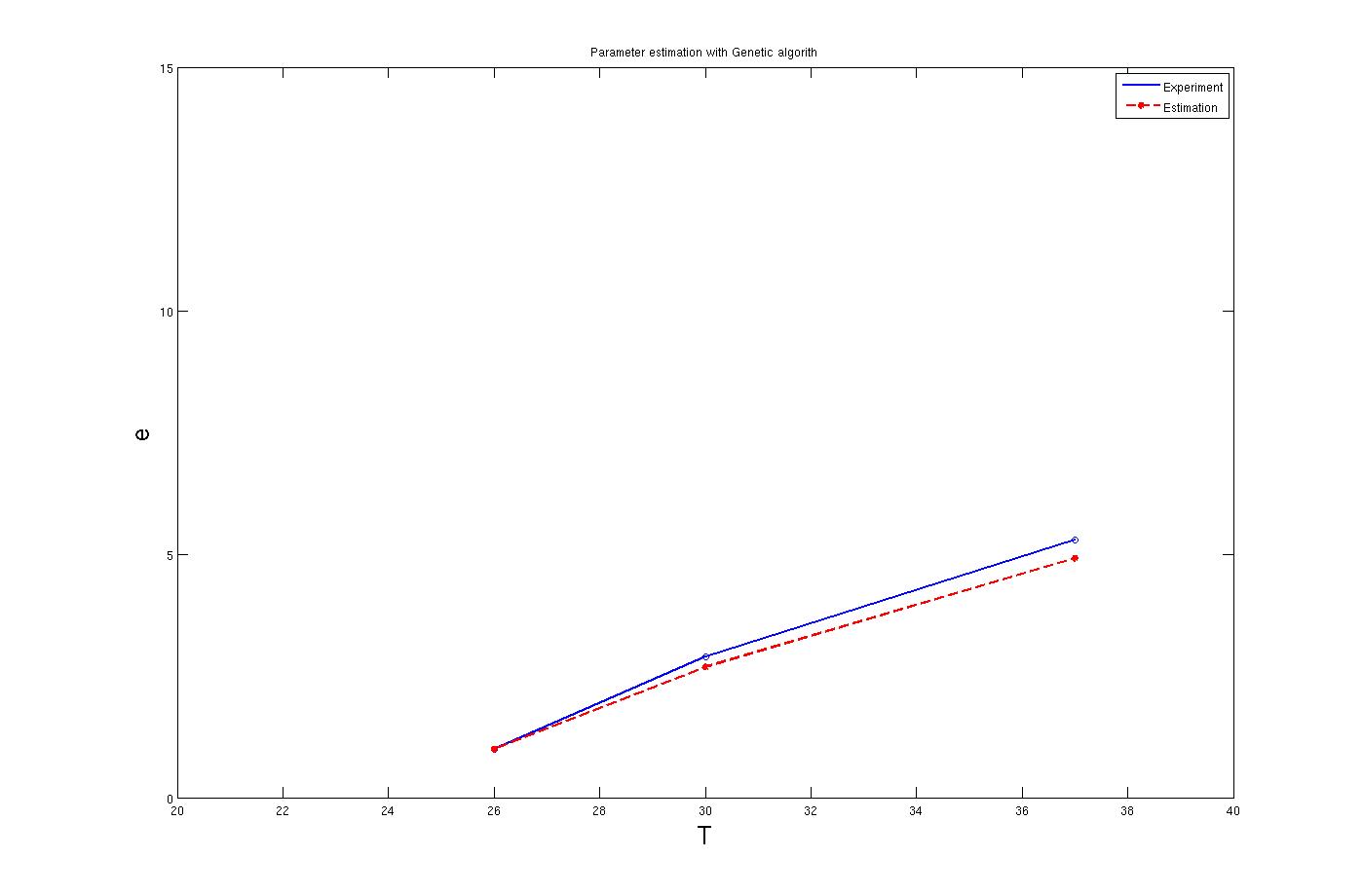
To find these parameters many solution like non linear set of equations has been tested. However the best results for the parameters has been concluded from the [http://en.wikipedia.org/wiki/Genetic_algorithm Genetic algorithm] search method. By this method parameters were estimated with a very good approximation. The calculations was based on the three points of the lab experiment results. The result for these method are shown in the graph below. The codes which includes the GA optimization method is available in the Download tab.
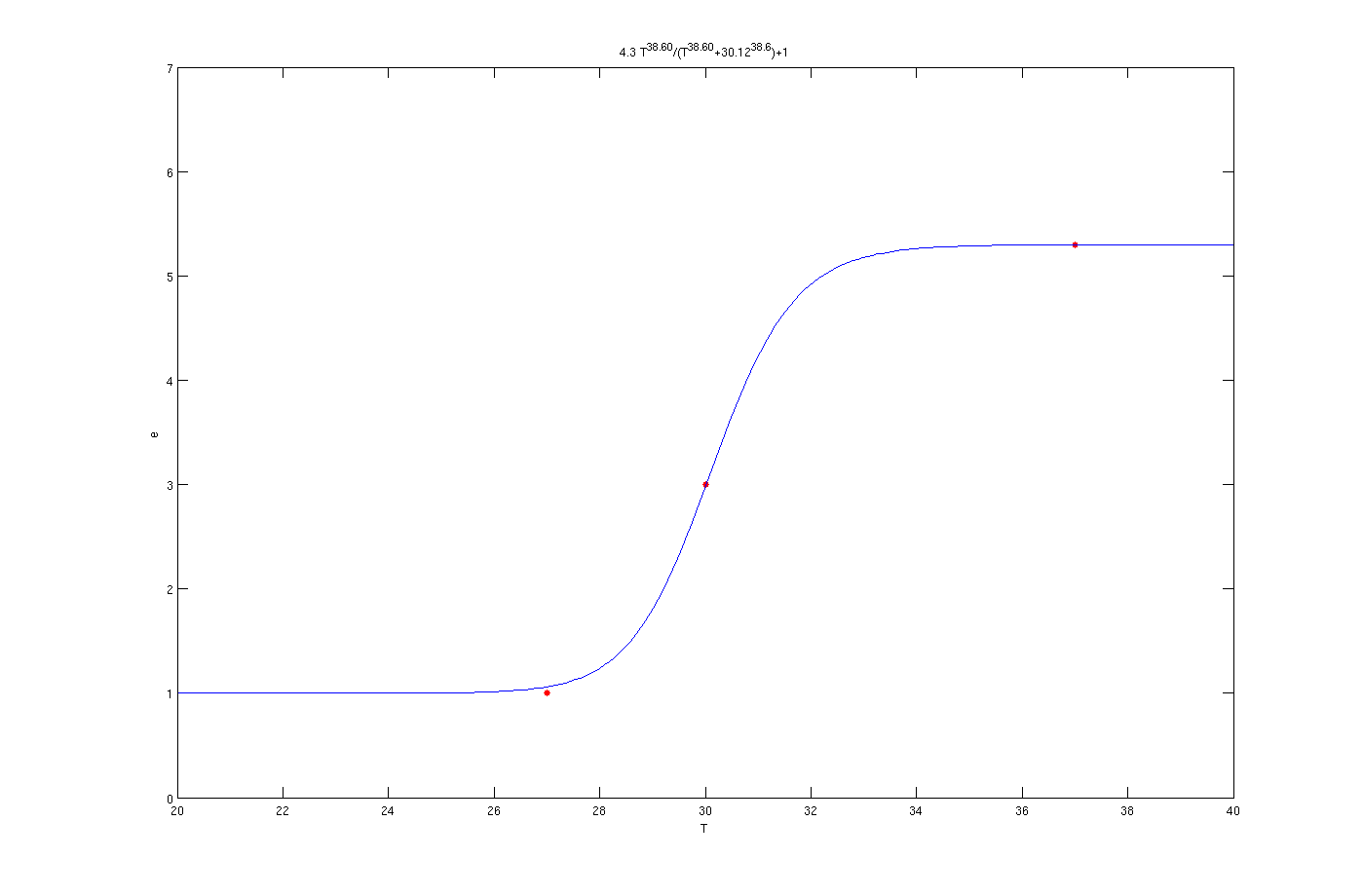
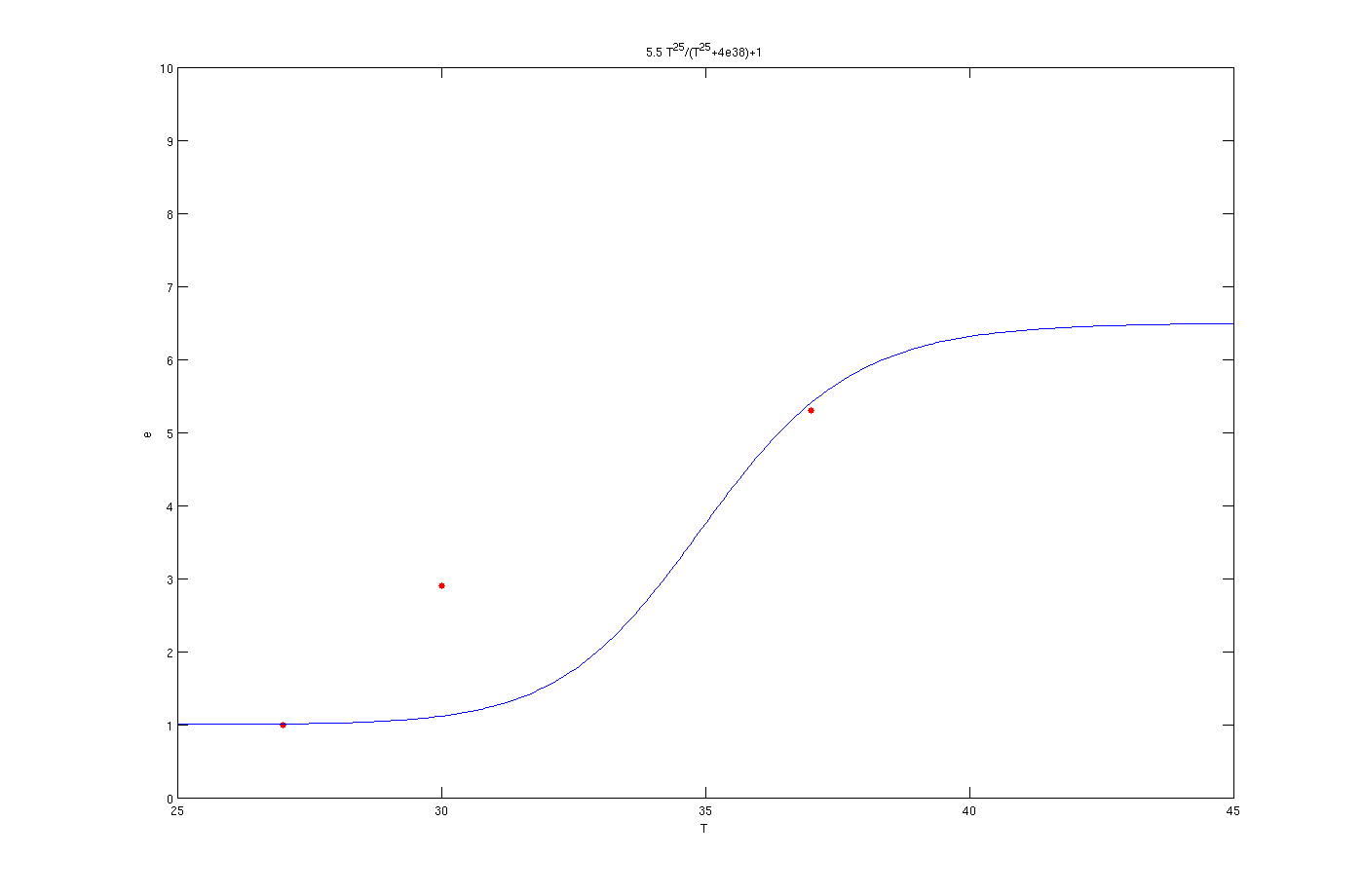
It is clear from the graph that the results are quite good. The enzyme concentration equation based on temperature for three enzymes which should activate at 27°C, 30°C and 37°C are shown below.
Enzyme activates at 27°C
Enzyme activates at 30°C
Enzyme activates at 37°C
In the above graphs, the red points are experimental results.
In the next step the enzymes inhibition is considered too. The general equation for the enzymes concentration with inhibition is:
The enzymes concentration and temperature are known but other parameters are unknown. It means that we have four points, but five unknows. In the first step we tried to solve the problem with the Genetic algorithm again. The amount of alpha consider to be known and the algorithm applied to calculate other parameters. Unfortunately results were not satisfactory.
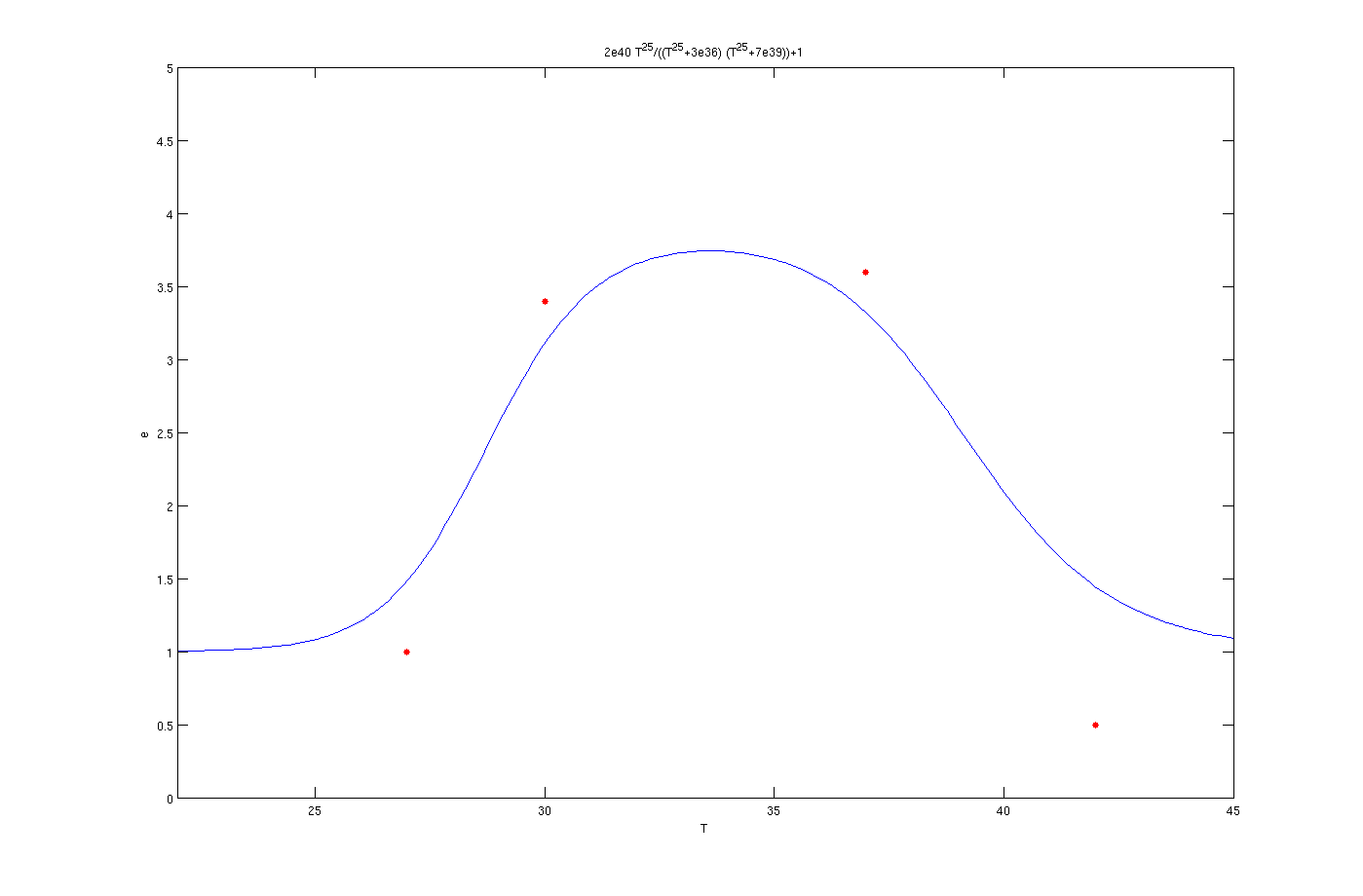
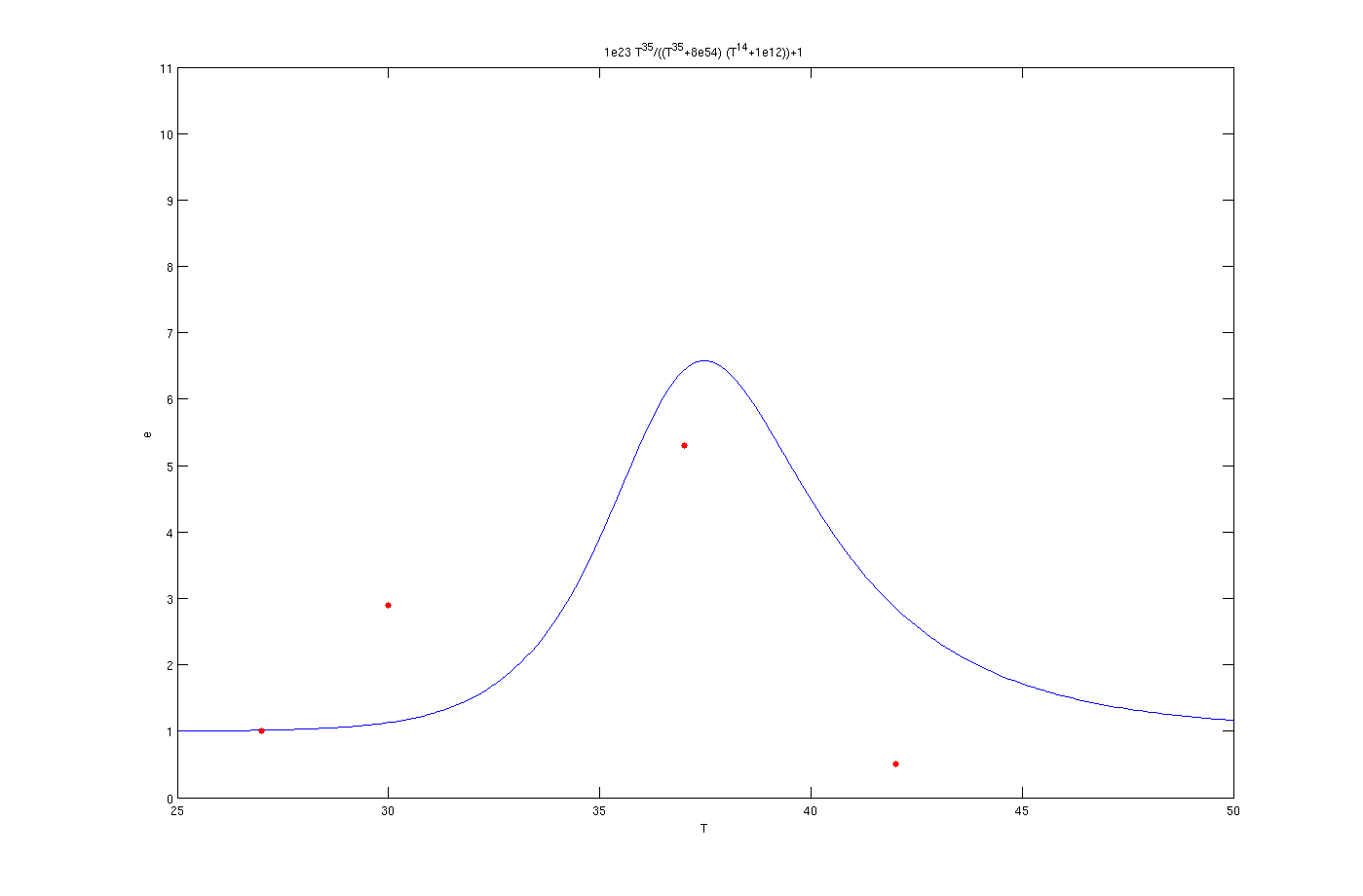
To solve this problem the try and error method has been used. Although this method is time consuming but the results are quite convincing. To use this method, one the parameters, for example m, has been assumed as known and other four was estimated by solving a set of four non linear equations. Afterwards another initially estimated parameter from the previous step assumed as known and other four has been estimated. This procedure was continued till it converged to a set of parameters. The enzyme concentrations with inhibition are:
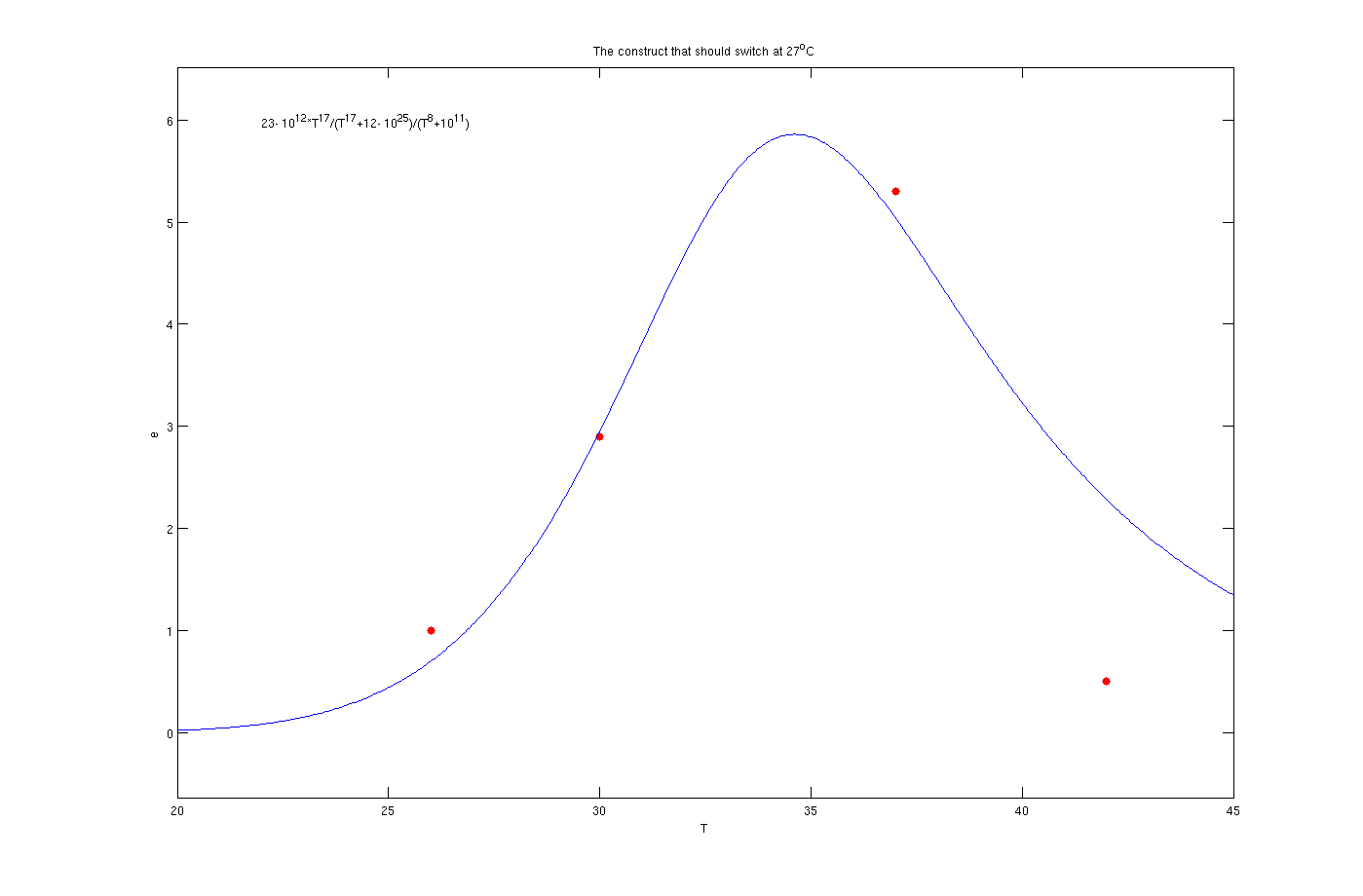
Enzyme activates at 27°C
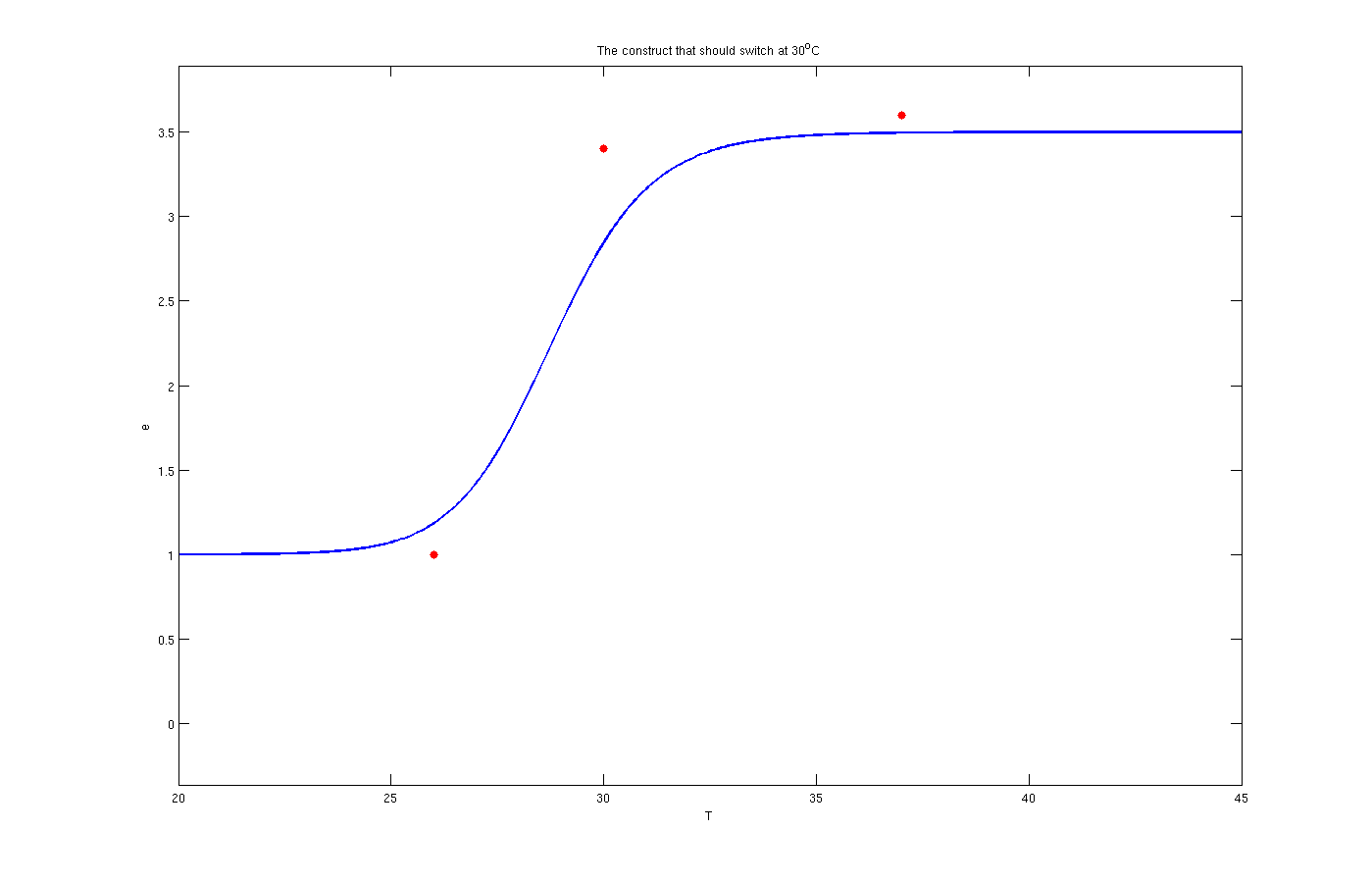
Enzyme activates at 30°C
Enzyme activates at 37°C
The red dots in the plots are the results from the lab. It is noticeable that the models work as switches that activated at 27°C, 30°C and 37°C.
Bifurcation and sensitivity analysis
To have a stable system it is important to do a bifurcation analysis to find the stable ranges for different reaction parameters. This procedure has been done by defining the parameters and substrates concentration as symbolic values in Matlab. Afterwards by these symbolic values the reactions are defined in symbolic format. By these symbolic reactions a vector for reaction ratios for different substrates can be derived. Afterwards by applying a specific steady state, which has been derived from previous step but by applying the initial parameters that have been found from the databases, and changing the reactions parameters in the range that has been found from the [http://www.brenda-enzymes.info/ data base] different reaction vectors were obtained. The changes in the parameter ranges has been define by a random selection in a normal distribution between 0.001 to 0.0374. Subsequently, different vectors for reactions can be derived from this step. The [http://en.wikipedia.org/wiki/Jacobian Jacobian] applied on each vector where the derivations were respect to the substrate and product concentrations. To conclude the stability for each situation it is necessary that all the [http://en.wikipedia.org/wiki/Eigenvalue,_eigenvector_and_eigenspace eigenvalues] of each Jacobian matrix be smaller than zero. If the condition is satisfied then the reactions and pathways are in the stable situation. By this method it is possible to find an approximate ranges for the reaction parameters.
As the last three products are important and to make the life easier, a lumped model has been designed for the pathway. Two approaches has been used for this procedure. The first one was calculating all the substrates concentration on the base of the first substrate concentration. This approach makes the model too complicated therefore it has been ignored. The second approach was combining all the substrates and enzymes before Phytoene as a single reaction. It means there is a reaction that has the Acetyl-CoA as input and Phytoene. With this lumped model it is easier to calculate the stability and do the sensitivity analysis for the model.
This pathway has been modeled in Matlab and the bifurcation analysis has been done. The model has been defined in Matlab symbolic therefore by substituting the parameters, enzymes concentrations and product concentrations with numbers, the stability can be derived. On the other hand the Jacobian matrix with respect to the products and substrates eigenvalues are always negative therefore it can be concluded that the pathway is always stable for the different values for parameters.
To do the sensitivity analysis on the model, the enzyme concentration equations have been implemented into the model. Afterwards the Jacobian respect to enzyme concentration parameters, α , m, K, p and Ki, has been calculated. All these calculations have been done in symbolic. Afterwards, all the parameters have been substituted by numbers. The results are shown below. The dimension of result matrix is 4 in 15. To make it easer to show and more clear it has been divided into three matrices. Each matrix, J1, J2 and J2, shows the results for one of the enzymes. In each matrix, each column shows the enzyme model sensitivity to parameters respectively α , m, K, Ki and p .
Results show, the models are highly sensitive to the amount of p in comparison to other parameters. This sensitivity is obvious in J3 which belongs to the last enzyme. Also the model is quite sensitive to the amount of K. The interesting point is that the model is not very sensitive to m as we thought before. On the other hand, the model is not sensitive to amount of α. This fact can be verify by the all first columns elements in three matrices where they are almost zero. Furthermore, the last enzyme model is not sensitive to Ki which is visible by the last column of the the last matrix. There are many zeros in the matrices, the reason is parameters ,for example, the first enzyme model are not participating in the second and third therefore the derivation respect to them is zero. The same reason can be concluded for other matrices elements which they are zero.
All the codes that have been used in bifurcation and sensitivity analysis are available through the Download tab.
Conclusion
The mathematical models for the production of enzymes could perfectly describe the experimental data as is obvious from the figures. The optimization algorithm finds the parameter values very well and the [http://en.wikipedia.org/wiki/Sum_of_squared_error SSE] is less than 1e-3. By inclusion of the inhibition terms we can see that the models show the switching behavior as expected. There are some points which are not in the switching regions like as the data point of 30° C in the plot of 37° C. This could be possibly due to measurement errors. Also the 42° C points are not in a close neighborhood of the curves. In all of figures the experimental value for 42° C is less than the one predicted by the model. The reason might be the behavior of living organisms at the extreme temperature of 42° C. According to sensitivity analysis the most important parameter of the function is p which is logical due to the fact that it considerably affects the derivative. Finally, in can be concluded that the overall view of the modeling part is satisfactory.
 "
"